Funciones polinomiales de grado 3 y 4.

FUNCIÓN CUBICA
–Comportamiento
final de sus graficas

FUNCIÓN CUBICA
 ,
,
Tanto el dominio de definición como el conjunto imagen de estas funciones pertenecen a los números reales.
La derivada de una función cúbica genera una función cuadrática y su integral una función cuártica.
Raíces reales de la ecuación cúbica
Partiendo de la ecuación canónica ) se elimina de la forma normal el término cuadrático y se obtiene la forma reducida:
) se elimina de la forma normal el término cuadrático y se obtiene la forma reducida: . La ecuación cúbica incompleta
. La ecuación cúbica incompleta 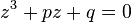 posee tres raíces reales cuando el discriminante
posee tres raíces reales cuando el discriminante 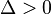 , pero donde
, pero donde  y
y 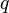 posee cualquier valor y signo. Tales raíces se calculan como
posee cualquier valor y signo. Tales raíces se calculan como , para
, para 
 y el signo negativo se usa si
y el signo negativo se usa si  . Mientras que
. Mientras que 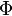 esta dada por
esta dada por , entonces podemos obtenerlas fácilmente como
, entonces podemos obtenerlas fácilmente como , para
, para 
Raíces múltiples
En cualquier ecuación cúbica es posible que se presenten raíces múltiples, es decir, raíces de multiplicidad dos y tres, esto es, que dos o tres de las raíces sean iguales entre sí. Las raíces de multiplicidad unitaria ya fueron descritas antes, ahora la raíz doble se puede presentar si y sólo si se cumple la condición de que .
.
El caso general
Sea un cuerpo conmutativo, donde se pueden extraer raíces, propiedad que hará posible resolver la ecuación.
un cuerpo conmutativo, donde se pueden extraer raíces, propiedad que hará posible resolver la ecuación.En un cuerpo algebraicamente cerrado se sabe que todo polinomio de tercer grado (o ecuación cúbica) tiene tres raíces. Este es el caso, por ejemplo, del cuerpo de los números complejos, según el Teorema Fundamental del Álgebra.
La solución de la ecuación algebraica cúbica fue dada por primera vez en el libro Ars Magna (del latín, que significa 'Gran Arte' o 'Arte Magno') por el matemático italiano Gerolamo Cardano (1501-1576) que publicó en el año de 1545, razón por la cual se le llama método de Cardano
Fórmula general
Dada la ecuación cúbicaSe calculan las siguientes cantidades:
En ese caso las tres raíces se pueden escribir simplemente como:
(*)
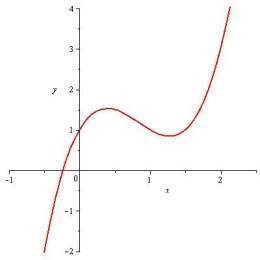

 | Identifica cada una de las siguientes gráficas con su expresión analítica. Descubre la expresión analítica de aquella que no consigas identificar. a) f(x) = x3 + 1 b) g(x) = x3 + 2x2 - x - 2 c) h(x)= -x3 + 4x2 - 4x |
La función cúbica "básica", f(x) = x3, está graficada a continuación.

La función del coeficiente a en la ecuación general es de hacer la gráfica "más amplia" o "más delgada", o de reflejarla (si es negativa):

La constante d en la ecuación es la intercepción en y de la gráfica.

Los efectos de b y c en la gráfica son más complicados. Sin embargo, si puede factorizar el lado derecho de la ecuación, puede encontrar una o más intercepciones en x, y usarlas para dibujar la gráfica. (Algunas cúbicas, sin embargo, no puede ser factorizadas.)

FUNCIÓN CUÁRTICA
 ) son números que pertenecen a un cuerpo, usualmente a los reales
) son números que pertenecen a un cuerpo, usualmente a los reales  o los complejos
o los complejos  .
.Sea K un cuerpo, donde se pueden extraer raíces cuadradas y cúbicas (y por lo tanto también de cuarto orden, pues equivale a extraer raíces cuadradas dos veces seguidas). En este cuerpo, es posible factorizar por todo a, y la identidad siguiente es válida:
 .
.
El método siguiente permite obtener las cuatro raíces al mismo tiempo. Este método es llamado "método de Descartes", pues fue dado por el matemático francés René Descartes (1596-1650) en el año de 1637 en su célebre libro "La Geometría". Aunque existan diferentes métodos para resolver las ecuaciones cuárticas, algunos son: método de Ferrari, método de Descartes, método de Euler, método de Lagrange, método de Alcalá, etcétera.
Método de Descartes
Los pasos de la resolución para el método de Descartes (1637) son:- Dividir la ecuación inicial por el coeficiente a. Se obtiene:
 , donde
, donde  ,
,  ,
,  y
y 
- Proceder al cambio de incógnita
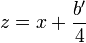 , para suprimir el término cúbico. En efecto, al desarrollar
, para suprimir el término cúbico. En efecto, al desarrollar  con la identidad precedente, vemos aparecer el término
con la identidad precedente, vemos aparecer el término 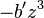 , compensado exactamente por
, compensado exactamente por  que aparece en
que aparece en  . Tras sustituir x y operando con las identidades notables, se obtiene:
. Tras sustituir x y operando con las identidades notables, se obtiene:
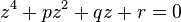 , con p, q y r números del cuerpo.
, con p, q y r números del cuerpo.
- Y ahora, la idea genial: factorizar lo anterior en
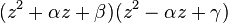 , lo que es posible porque no hay z³ en el polinomio.
, lo que es posible porque no hay z³ en el polinomio.
 (coeficiente de x²)
(coeficiente de x²) (coeficiente en x)
(coeficiente en x) (término constante)
(término constante)
 Es una ecuación de sexto grado, pero si miramos bien, α sólo aparece con potencias pares.
Es una ecuación de sexto grado, pero si miramos bien, α sólo aparece con potencias pares.Pongamos
 . Entonces:
. Entonces: , que resulta ser una ecuación de tercer grado en la variable
, que resulta ser una ecuación de tercer grado en la variable  y que se puede resolver usando el método de Cardano.
y que se puede resolver usando el método de Cardano.
 y
y 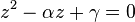 , y para terminar, no olvide que
, y para terminar, no olvide que  .
.EJERCICIOS:
FUNCION: F(X)= (x+4)(x+1)(x-1)(x-3) + 0.5 F(X)=x^4+x^3-13 x^2-x+12.5
GRAFICO:
ANALISIS
- DOMINIO: todos los valores que puede tomar la variable independiente x. En este caso: todos los reales.
- IMAGEN: son todos aquellos valores que puede tomar la variable dependiente y.En este caso todos los reales.
- RAICES: los numeros que puede tomar la variable x para que la funcion sea igual a 0, es decir: f(x)=o en este caso las raices son: -4;-1;1 y 3

- ORDENADA AL ORIGEN: todos aquellos valores de y para cuando x=0. En este caso: 12,5
- CONJUNTO DE POSITIVIDAD: conjunto de valores de x tales que f(x)<0 (aclaracion: oo= a infinito) (-OO; -4) U (-1;1) U (3;OO)
- CONJUNTO DE NEGATIVIDAD: conjuto de valores de x tales que f(x)>0 (-4;-1) U (1;3)
- INTERVALO DE CRECIMIENTO: (-3;0) U (3;OO)
- INTERVALO DE DECRECIMIENTO: (-OO;-3) U (0;3)
- MAXIMO Y MINIMO: para realizar esa operacion, primero hay que derivar la funcion y una vez derivada el programa la analiza y nos da los punto criticos, los cuales luego son reemplazados en la funcion original para saber uales son los maximos y/o minimos.
FUNCIÓN POLINOMICA DE GRADO 4:
Al tener esta información y ver el gráfico, determiné lo siguiente:
Conjunto de positividad: (- ;-1) U (2;3) U (5;
;-1) U (2;3) U (5; )
)
 ;-1) U (2;3) U (5;
;-1) U (2;3) U (5; )
)
Conjunto de negatividad: (-1;2) U (3;5)
Al igualar fa función a 0, resolví que la ordenada al origen es -30
Para sacar los máximos y los mínimos, calculé la derivada:

a partir de ella, obtuve 3 raíces, que son los puntos críticos: -0,023 ; 2,486 ; 4,287
al reemplazarlos en la función obtuve los siguientes puntos, que luego verifique observando el gráfico:
Máximo local: (2,486 ; 2,189)
Mínimos locales: (-0,023 ; -30,012) (4,287 ; -11,095)
Luego viendo el comportamiento de la curva y teniendo en cuenta los máximos y los mínimos, determiné lo siguiente:
Intervalos de crecimiento: (-0,023 ; 2,486) U (4,287; )
)
 )
)
Intervalos de decrecimiento: (- ;-0,023) U (2,486;4,287)
;-0,023) U (2,486;4,287)
 ;-0,023) U (2,486;4,287)
;-0,023) U (2,486;4,287)
Por último, la imagen la la función son todos los números reales mayores o iguales a -30,012
Funcion: f(x)=x^4-2 x^3-3 x^2+4 x+4
- Dominio. IR
- Imagen. IR>0
- Raíces. -1;2
- Ordenada al origen. 4
- Conjuntos de positividad (-∞;-1) u (-1;2) u (2; ∞)
- Negatividad.-
- Máximos y mínimos. ESTA ABAJO
- Intervalos de crecimiento (-1;0,5) u (2;∞)
- Decrecimiento. (-∞;-1) u (0.5;2)
Para hallar los máximos y mínimos debemos averiguar la derivada de la función:
F’(x)= 4x^3-6x^2-6x+4
Luego para obtener el primer punto critico demos hacer Gauss
P= ±4; ±2; ±1
Q=±4; ±2; ±1
P/Q: -1
Ahora se reemplaza los valores en la función original.
2^4-2 2^3-3 2^2+4 2+4= 0
0.5^4-2 0.5^3-3 0.5^2+4 0.5+4= 5,06
-1^4-2 -1^3-3 -1^2+4 -1+4= 0
Ahora hay que hacer la subderivada y reemplazar los valores para saber maximos y minimos.
F’’(x)=12x^2-12x-6
Máximos: 5,06
Mínimos: 0; 0
función: x^4 - 5x^3 + 5x^2 + 5x - 6
Gráfico: 

raíces: -1, 1, 2 y 3
Para hallar las raíces,primero (teorema de gauss) busque p/q= 1/1(f (1)=0), entonces sabia que una raíz era (x-1), luego realice el teorema de Ruffini y me queda la siguiente función x^3-4x^2-x+6 , a esta misma la factoreo y me queda (x+1)* (x^2-4x-1), allí encontré otra raíz (x+1), luego realizo la formula matemática: –b -+ raíz de –b^2-4*a*c sobre 2*a y me dan las dos raíces que faltan ( 2 y 3)
c+: (-oo;-1) u (1;2) u (3; oo)
c-: (-1;1) u (2;3)
intervalo de Crecimiento: ( -0,3 aprox; 1,5 aprox) u (2,5 aprox; oo)
intervalo de De crecimiento: (-oo; -0,3) u (1,5 aprox; 2,5 aprox)
Dominio: IR
imagen: IR < -0,3 aprox
Ordenada al origen: -6
Mínimo:( -0,3 ; 6,9)
 Máximo: (1,5 ; 0,9 ) aprox
Máximo: (1,5 ; 0,9 ) aprox Derivada:







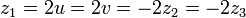


![\begin{matrix} Q=\cfrac{3a_2-a_1^2}{9}, & R=\cfrac{9a_1a_2-27a_3-2a_1^3}{54} \\
S_1= \left[ R + \sqrt{Q^3+R^2} \right]^{1/3}, & S_2= \left[ R - \sqrt{Q^3+R^2} \right]^{1/3}
\end{matrix}](http://upload.wikimedia.org/math/3/8/8/388700a17ed67b13a99c481709c27552.png)








No hay comentarios.:
Publicar un comentario