Teorema de los ceros complejos.
Los ceros complejos de polinomios con coeficientes reales, si existen, se presentan en pares conjugados.
Como consecuencia del teorema anterior, se sabe que si un polinomio con coeficientes reales es de grado impar, siempre tiene al menos un cero real.
Ejercicios:
Si  es un polinomio de tercer grado con
coeficientes reales, entonces una de las siguientes afirmaciones es falsa:
es un polinomio de tercer grado con
coeficientes reales, entonces una de las siguientes afirmaciones es falsa:
a.  tiene al menos un cero real.
tiene al menos un cero real.
b.  tiene tres ceros.
tiene tres ceros.
c.  puede tener dos ceros reales y uno
complejo
puede tener dos ceros reales y uno
complejo
Teorema de los residuos
EJERCICIOS:
f ( x ) = x2 - 8 x + 6. Divida el polinomio entre el binomio x - 2.
f ( x ) = x2 - 8 x + 6. Divida el polinomio entre el binomio x - 2.
División larga
 .
.El residuo es -6.
Método 2: División sintética

El residuo es -6.
Ahora compare el residuo de -6 en f (2).

si f(x) = x2 + x - 2 se divide entre (x-2)
el residuo es f(2) = 22 + (2) - 2 = 4.
Este resultado puede volverse obvio si cambiamos el polinomio a una de las siguientes formas equivalentes:
f(x) = (x-2)(x+3) + 4
Teorema del Factor.
El teorema del factor sirve para encontrar los factores de un polinomio (una expresión en la cual los términos sólo son sumados, sustraídos o multiplicados, e.g.  ). Es un caso especial del teorema del resto.
). Es un caso especial del teorema del resto.
 ). Es un caso especial del teorema del resto.
). Es un caso especial del teorema del resto.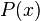 tiene un factor
tiene un factor  si y sólo si
si y sólo si  es una raíz de
es una raíz de 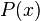 , es decir que
, es decir que  .
.EJERCICIOS:
Sii se desea encontrar los factores de
 , para ello se podría tantear un primer factor,
, para ello se podría tantear un primer factor, 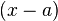 . Si el resultado de sustituir
. Si el resultado de sustituir  en el polinomio es igual a 0, se sabe que hay un factor. ¿Es
en el polinomio es igual a 0, se sabe que hay un factor. ¿Es  un factor? Para saberlo, se sustituye
un factor? Para saberlo, se sustituye 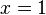 en el polinomio:
en el polinomio: no es un factor de
no es un factor de  . Así que ahora se prueba con
. Así que ahora se prueba con  (sustituyendo
(sustituyendo 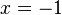 en el polinomio):
en el polinomio): .
.
 , que es equivalente a
, que es equivalente a 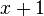 , es un factor, y -1 es una raíz de
, es un factor, y -1 es una raíz de  .
.Las otras dos raíces se pueden encontrar dividiendo
 entre
entre  para obtener un polinomio de segundo grado, que se puede resolver de la siguiente manera
para obtener un polinomio de segundo grado, que se puede resolver de la siguiente manera 
ademas el teorema del factor es muy factible para estos casos
Comprueba que los siguientes polinomios tienen como factores los que se indican:
(x3− 5x − 1) tiene por factor (x − 3)
(x3 − 5x −1) es divisible por (x − 3) si y sólo si P(x = 3) = 0.
P(3) = 33 − 5 · 3 − 1 = 27 − 15 − 1 ≠ 0
(x − 3) no es un factor.
2(x6 − 1) tiene por factor (x + 1)
(x6 − 1) es divisible por (x + 1) si y sólo si P(x = − 1) = 0.
P(−1) = (−1)6 − 1 = 0
(x + 1) es un factor.
3(x4− 2x3 + x2 + x − 1) tiene por factor (x − 1)
(x4 − 2x3 + x2 + x − 1) es divisible por (x − 1 ) si y sólo si P(x = 1) = 0.
P(1) = 14 − 2 · 13 + 1 2 + 1 − 1 = 1 − 2 + 1 + 1 − 1 = 0
(x − 1) es un factor.
4(x10 − 1024) tiene por factor (x + 2)
(x10 − 1024) es divisible por (x + 2) si y sólo si P(x = − 2) = 0.
P(−2) = (−2)10 − 1024 = 1024 − 1024 = 0
(x + 2) es un factor
Use el teorema del factor para probar que
Solución.
Luego –1 es un cero de
Así
DIVISIÓN SINTETICA.
El procedimiento que usaremos para realizar la división sintética de un polinomio
EJERCICIOS :
Sean
Determine el cociente y el residuo que se obtiene al dividir
a) Usando el método estudiado anteriormente (División larga)
b) Usando división sintética
Solución:
a)

| Por lo que al dividir |
b) Usando división sintética,  se divide por
se divide por  de la siguiente manera:
de la siguiente manera:
 Donde los números 4, 15 y 40 son los coeficientes del cociente y 122 el
residuo de la división.
Observe que, según la parte (a) de este ejercicio, los números obtenidos en
la tercera fila son los coeficientes del cociente y el residuo, como se muestra
en el esquema anterior.
Los números representados en la primera fila son los coeficientes de
Donde los números 4, 15 y 40 son los coeficientes del cociente y 122 el
residuo de la división.
Observe que, según la parte (a) de este ejercicio, los números obtenidos en
la tercera fila son los coeficientes del cociente y el residuo, como se muestra
en el esquema anterior.
Los números representados en la primera fila son los coeficientes de
Los números representados en la segunda fila se obtienen de la siguiente
forma:
12 es el producto de 4 y 3
45 es el producto de 15 y 3
120 es
el producto de 40 y 3
Los números representados en la tercera fila se obtienen de la siguiente
forma:
4 es el coeficiente de  en
en 
15 es la suma de 3 y 12
40 es la
suma de -5 y 45
122 es la suma de 2 y 120
Donde -108 es el residuo
Donde 748 es el residuo y pese a no tener muchos coheficientes vemos que en el resultado si aparecen todos los coheficientes nesesarios para todos los exponentes.
el polinomio x4 - 11x3 + 26x2 + 44x
- 120 entre el polinomio x + 2.
Los coeficientes del polinomio son [1 -11 26
44 120] y a = −2 porque x + 2 = x − (−2) = x − a. La división
sintética queda así:

Cociente: x3 - 13x2 + 52x -
60.
Residuo: 0.
la división es exacta, por eso el residuo es cero.
Residuo: 0.
la división es exacta, por eso el residuo es cero.
Dividir el polinomio x3
+ 1 entre el polinomio x − 1.
Los coeficientes del polinomio son [1 0 0
1] (observar como se insertan ceros en las posiciones de los términos con
x2 y x) y a = 1. La división sintética queda
así:

Cociente: x2 + x + 1.
Residuo: 2.
Residuo: 2.
el polinomio 2x4 - 3x3 - 15x2 - 10x + 6
entre el polinomio x - 3.

. El último número es el residuo y los números anteriores son los coeficientes del cociente de orden n - 1.

Cociente: 2x3 + 3x2 - 6x - 28.
Residuo: - 78.
2x4 - 3x3 -
15x2 - 10x + 6 = (x - 3) (2x3
+ 3x2 - 6x - 28) - 78
Teorema de la Factorización Líneal.
Cualquier polinomio cuyo grado n esté definido tendrá exactamente n factores lineales
Prueba del cero racional
En álgebra, el teorema de la raíz racional o la prueba de la raíz racional indica una restricción en las soluciones racionales (o raíces) de la ecuación polinómica con coeficientes enteros:
- p es un factor del término constante a0, y
- q es un factor del coeficiente del término an.

EJERCICIOS:
y = 0
Entonces:
x³ - 31x² + 30 = 0 ← Acá factorizamos como producto de Binomio por Trinomio:
(x - 1)(x² - 30x - 30) = 0 ← Igualando a cero cada factor, se tienen las raíces de "x":
x - 1 = 0 ======> x₁= 1
x² - 30x - 30 = 0 ← Acá aplicamos la fórmula cuadrática:
…………... ______
….... -b + √b² - 4ac
x₂= ------------------ ====> Con a= 1 .... b= -30 .... c= -30
…………. 2a
……………..... ______________
……. -(-30) + √[-30]² - 4*1*(-30)
x₂= ------------------------------------ =
……………….... 2*1
………….... ________ ............. ____
……. 30 + √900 + 120 ... 30 + √1020
x₂= ----------------------- = ---------------- =
…………….. 2 ....................... 2
….... 30 + 31,937439 .... 61,937439
x₂= ---------------------- = --------------- =
…………..... 2 ...................... 2
x₂≈ 30,96872
….... 30 - 31,937439 ... -1,937439
x₃= --------------------- = -------------- =
.................. 2 ...................... 2
x₃≈ -0,96872
Si –2 es un cero de multiplicidad 2 de  , escríbase
, escríbase  como un producto de factores lineales.
como un producto de factores lineales.
Solución.
Como –2 es un cero de multiplicidad 2, se tiene que,
Al usar la formula cuadrática, se hallan los ceros de  que son
que son  ,
,
 .
.
Así,  escrito como el producto de factores lineales
es,
escrito como el producto de factores lineales
es,
Teorema Fundamental del Álgebra
El teorema fundamental del álgebra establece que un polinomio en una variable, no constante y con coeficientes complejos, tiene tantas raíces como indica su grado, contando las raíces con sus multiplicidades. En otras palabras, dado un polinomio complejo  de grado
de grado 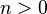 , la ecuación
, la ecuación  tiene exactamente
tiene exactamente  soluciones complejas, contando multiplicidades. De manera equivalente:
soluciones complejas, contando multiplicidades. De manera equivalente:
 de grado
de grado 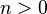 , la ecuación
, la ecuación  tiene exactamente
tiene exactamente  soluciones complejas, contando multiplicidades. De manera equivalente:
soluciones complejas, contando multiplicidades. De manera equivalente:- El cuerpo de los complejos es cerrado para las operaciones algebraicas.
- Todo polinomio complejo de grado n se puede expresar como un producto de n polinomios de la forma
 .
.
El teorema se establece comúnmente de la siguiente manera:
Todo polinomio en una variable de grado n ≥ 1 con coeficientes reales o complejos tiene por lo menos una raíz (real o compleja). |
Aunque ésta en principio parece ser una declaración más débil, implica fácilmente la forma completa por la división polinómica sucesiva por factores lineales.
EJERCICIOS:
Encontrar la solución de la siguiente ecuación: y=2x+1
Para poder encontrar las soluciones reales, debemos cruzar esa recta con el eje x, esto implica hacer y=0:
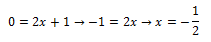
Para este caso en concreto, vemos que esta ecuación, solo tiene una única solución, -1/2
.
Según el teorema, si el grado es impar, tenemos al menos una raíz real.
Para entenderlo, vamos a reescribirlo de esta manera:
Un polinomio de grado n impar admite al menos una raíz real. Si existe una raíz compleja 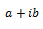 de un polinomio, entonces existe su raíz compleja conjugada
de un polinomio, entonces existe su raíz compleja conjugada 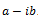
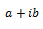 de un polinomio, entonces existe su raíz compleja conjugada
de un polinomio, entonces existe su raíz compleja conjugada 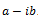
En el ejemplo anterior, era una ecuación de grado uno (mirad el exponente de las x), por lo que el número mínimo de raíces va a ser 1. Lo cual no quiere decir que tenga que haber solamente una raíz, puede haber más, pero siempre será ese mínimo

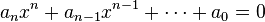
No hay comentarios.:
Publicar un comentario