Función Logaritmica.
(esto se lee como: logaritmo en base b de x es igual a n; si y sólo si b elevado a la n da por resultado a x)
Para que la definición sea válida, no todas las bases y números son posibles. La base b tiene que ser positiva y distinta de 1, luego b> 0 y b ≠ 1, x tiene que ser un número positivo x > 0 y n puede ser cualquier número real (n ∈ R).[2]
Así, en la expresión 102 = 100, el logaritmo de 100 en base 10 es 2, y se escribe como log10 100 = 2.
Propiedades generales
Los logaritmos, independientemente de la base elegida, cumplen una serie de propiedades comunes que los caracterizan.Así, logaritmo de su base es siempre 1; logb b = 1 ya que b1 = b. El logaritmo de 1 es cero (independientemente de la base); logb 1=0 ya que b0 = 1.
Si el número real a se encuentra dentro del intervalo 0 < a < 1 entonces logb a da un valor negativo o se dice que es un logaritmo negativo. Es evidente, ya que si logaritmo de 1 es cero, entonces valores reales menores que uno serán negativos por ser la función logarítmica estrictamente creciente y cuyo recorrido es (-∞, +∞). También se puede demostrar usando la identidad logarítmica logb(x/y)=logb x - logb y; puesto que a pertenece al intervalo 0 < a < 1, su inverso a-1 será mayor que uno, con lo que logb(a)=logb(1/a-1) = logb 1 - logb(a-1)= -logb(a-1).
Los números negativos no tienen logaritmo en el cuerpo de los reales R, ya que cualesquiera que sea el exponente n, se tendrá siempre que bn será mayor que cero, bn > 0; en consecuencia, no hay ningún valor real de n que pueda satisfacer bn = x cuando x sea menor que 0. Sin embargo, este obstáculo se puede salvar, ampliando el dominio de definición al cuerpo de los números complejos C, pudiendo calcular logaritmos de números negativos usando el logaritmo complejo o recurriendo a la fórmula de Euler.
Los logaritmos mantienen ciertas identidades aritméticas muy útiles a la hora de realizar cálculos:
- El logaritmo de un producto es igual a la suma de los logaritmos de los factores.
- El logaritmo de un cociente es igual al logaritmo del numerador menos el logaritmo del denominador.
- El logaritmo de una potencia es igual al producto entre el exponente y el logaritmo de la base de la potencia.
- El logaritmo de una raíz es igual al producto entre la inversa del índice y el logaritmo del radicando.
Gráfico de la función logarítmica logb(x) (azul) se obtiene mediante reflexión del gráfico de la función bx (roja) sobre la línea diagonal (x = y).
EJERCICIOS:
EJERCICIOS:
f (x) = log 2 (x +
2)
- Determine el dominio de f y el rango de f.
- Encuentra la asíntota vertical de la gráfica de f.
- Encuentra la X y la intercepta y de la gráfica de f si los hay.
- Dibuje la gráfica de f.
Respuesta a la Ejemplo 1
a - El dominio de f es el conjunto de todos los
valores de x tal que
x + 2 > 0
x > -2
El rango de f es el intervalo (-inf, +
inf).
b - La asíntota vertical se obtiene mediante la
solución de
x + 2 = 0
lo que da
x = -2
Cuando x tiende a -2 de la derecha (x> -2), f
(x) decrece sin límite. ¿Cómo sabemos esto?
Veamos algunos valores:
f (-1) = log 2 (-1 + 2) = log
2 (1) = 0
f (-1,5) = log 2 (-1,5 + 2) = log
2 (1 / 2) = -1
f (-1,99) = log 2 (-1,99 + 2) = log
2 (0.01), que es aproximadamente igual a -6,64
f (-1.999999) = log 2 (-1,999999 + 2)
= log 2 (0.000001), que es aproximadamente igual a -19,93.
c - Para encontrar la intersección x tenemos que
resolver la ecuación f (x) = 0
log2 (x + 2) = 0
Usar las propiedades de las funciones
logarítmicas y exponenciales para escribir la ecuación anterior como
x + 2 = 2^0
x = -1
La intersección x es (-1, 0).
La intersección está dada por (0, f (0)) = (0,
log 2 (0 + 2)) = (0, 1).
d - Hasta ahora tenemos el dominio, rango, x e
intercepta y, y la asíntota vertical. Necesitamos más
puntos. Vamos a considerar un punto en x = -3 / 2 (a
medio camino entre la X y la intersección de la asíntota vertical) y otro punto
en x = 2.
f (-3 / 2) = log 2 (-3 / 2 + 2) = log
2 (1 / 2) = log 2 (2 -1) = -1.
f (2) = log 2 (2 + 2) = log
2 (2 2) = 2.
Ahora tenemos más información sobre la forma de
gráfico de f. El gráfico aumenta a medida que aumenta x.
Cerca de la asíntota vertical x = -2, la gráfica de f
disminuye sin límite cuando x tiende a -2 de la derecha. La gráfica no corta la asíntota vertical. Nos
unen ahora a los diferentes puntos de una curva suave.
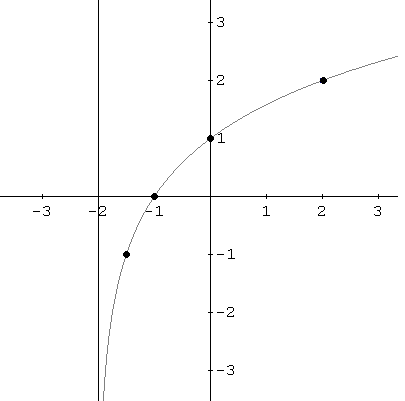
f (x) = log 2 (x + 3)
- Determine el dominio de f y el rango de f.
- Encuentra la asíntota vertical de la gráfica de f.
- Encuentra la X y la intercepta y de la gráfica de f si los hay.
- Dibuje la gráfica de f.
Ejemplo 2: f es una función dada por
f (x) = -3ln (x - 4)
- Determine el dominio de f y el rango de f.
- Encuentra la asíntota vertical de la gráfica de f.
- Encuentra la X y la intercepta y de la gráfica de f si los hay.
- Dibuje la gráfica de f.
Respuesta a la Ejemplo 2
a - El dominio de f es el conjunto de todos los
valores de x tal que
x - 4 > 0
x > 4
El rango de f es el intervalo (-inf, +
inf).
b - La asíntota vertical se obtiene mediante la
solución de
x - 4 = 0
x = 4
Cuando x tiende a 4 de la derecha (x> 4), f
(x) crece sin límite. ¿Cómo sabemos esto?
Veamos algunos valores:
f (5) = ln (5-4) =-3ln (1) = 0
f (4,001) =-3ln (0,001), que es aproximadamente
igual a 20,72.
f (4.000001) =-3ln (0,000001), que es
aproximadamente igual a 41,45.
c - Para encontrar la intersección x tenemos que
resolver la ecuación f (x) = 0
-3ln(x - 4) = 0
Divide ambos lados por -3 a obtener
ln (x - 4) = 0
Usar las propiedades de las funciones
logarítmicas y exponenciales para escribir la ecuación anterior como
e ln (x - 4) = e
0
Luego de simplificar
x - 4 = 1
x = 5
La x es interceptar en (5, 0).
La intersección está dada por (0, f (0)). f (0)
no está definido ya que x = 0 no es un valor en el dominio de f. No hay ninguna intersección.
d - Hasta ahora tenemos el dominio, rango, x
interceptar y la asíntota vertical. Necesitamos puntos
extra para poder gráfico de f.
f (4,5) =-3ln (4,5 - 4) aproximadamente igual a
2,08
F (8) =-3ln (8 - 4) aproximadamente igual a -
4,16
f (14) =-3ln (14 - 4) aproximadamente igual a -
6,91
Veamos ahora esbozar todos los puntos y la
asíntota vertical. Únete a los puntos por una curva
suave y F aumenta a medida que x se aproxima a 4 de la derecha.

f (x) = 2ln (x + 5)
- Determine el dominio de f y el rango de f.
- Encuentra la asíntota vertical de la gráfica de f.
- Encuentra la X y la intercepta y de la gráfica de f si los hay.
- Dibuje la gráfica de f.
Ejemplo 3: f es una función dada por
f (x) = 2ln (| X |)
- Determine el dominio de f y el rango de f.
- Encuentra la asíntota vertical de la gráfica de f.
- Encuentra la X y la intercepta y de la gráfica de f si los hay.
- Dibuje la gráfica de f.
Respuesta a la Ejemplo 3
a - El dominio de f es el
conjunto de todos los valores de x tal que
|x| > 0
El dominio es el conjunto de todos los números
reales excepto 0.
El rango de f es el intervalo (-inf, +
inf).
b - La asíntota vertical se obtiene mediante la
solución de
|x| = 0
lo que da
x = 0
Cuando x tiende a 0 por la derecha (x> 0), f
(x) decrece sin límite. ¿Cómo sabemos esto?
Veamos algunos valores:
f (1) = 2 ln (| 1 |) = 0
f (0,1) = 2ln (0,1), que es aproximadamente igual
a -4,61.
f (0,0001) = 2ln (0,0001), que es aproximadamente
igual a -18,42.
f (0.0000001) = 2ln (0,0000001), que es
aproximadamente igual a -32,24.
Cuando x se aproxima a 0 por la izquierda (x
<0), f (x) decrece sin límite. ¿Cómo sabemos
esto?
Veamos algunos valores:
f (-1) = 2 ln (| -1 |) = 0
f (-0,1) = 2ln (| -0,1 |), que es aproximadamente
igual a -4,61.
f (-0,0001) = 2ln (| -0,0001 |), que es
aproximadamente igual a -18,42.
f (-0.0000001) = 2ln (| -0,0000001 |), que es
aproximadamente igual a -32,24.
c - Para encontrar la intersección x tenemos que
resolver la ecuación f (x) = 0
2ln (| X |) = 0
Divide ambos lados por 2 para obtener
ln (| X |) = 0
Usar las propiedades de las funciones
logarítmicas y exponenciales para escribir la ecuación anterior como
e ln (| X |) = e
0
Luego de simplificar
| X | = 1
Dos x intercepta en (1, 0) y
(-1, 0).
La intersección está dada por (0, f (0)). f (0)
no está definido ya que x = 0 no es un valor en el dominio de f. No hay ninguna intersección.
d - Hasta ahora tenemos el dominio, rango, x
interceptar y la asíntota vertical. Mediante el examen
de la función f es fácil demostrar que esta es una función par y su gráfica es
simétrica con respecto al eje y.
f (-x) = 2 ln (|-x |)
pero
|-x | = | x |
y por lo tanto
f (-x) = 2 ln (| x |) = f (x), esto demuestra
que f es una función par.
Vamos a encontrar puntos extra.
f (4) = 2ln (| 4 |) aproximadamente igual a
2,77.
f (0,5) = 2ln (| 0.5 |) aproximadamente igual a -
1,39.
Como f es aún f (-4) = f (4) y f (-0,5) = f
(0,5).
Veamos ahora esbozar todos los puntos, la
asíntota vertical y Una los puntos por una curva suave.
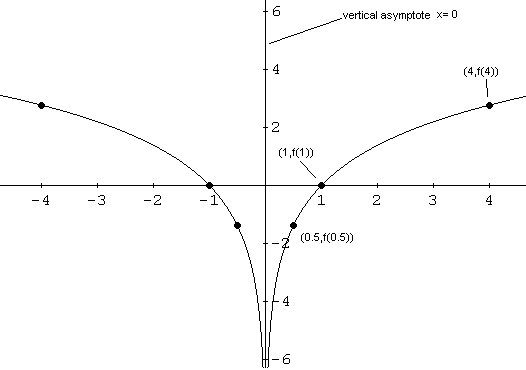
a.
| x | |
|---|---|
| 1/8 | -3 |
| 1/4 | -2 |
| 1/2 | -1 |
| 1 | 0 |
| 2 | 1 |
| 4 | 2 |
| 8 | 3 |

| x | |
|---|---|
| 1/8 | 3 |
| 1/4 | 2 |
| 1/2 | 1 |
| 1 | 0 |
| 2 | −1 |
| 4 | −2 |
| 8 | −3 |

Función Exponencial.
En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma
Propiedades
- Son las únicas funciones que son igual a su derivada (multiplicada por una constante, en el caso de que tengan una base distinta a e)



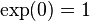
El dominio son los números reales
y el recorrido son los reales positivos
• Es continua en todo el dominio
• Si a>1 la función es creciente en todo su dominio
• Si 0<a<1 la función es decreciente
• Corta al eje OY en el punto (0,1)
• El eje OX es una asíntota horizontal
Aplicaciones
La función exponencial sirve para describir cualquier proceso que evolucione de modo que el aumento (o disminución) en un pequeño intervalo de tiempo sea proporcional a lo que había al comienzo del mismo. En la escena puedes ver tres aplicaciones:
- Crecimiento de poblaciones.
- Interés del dinero acumulado.
- Desintegración radioactiva.
Algunas
características de las funciones exponenciales
crecientes:
1) El
dominio es el conjunto de los números reales.
2) El
recorrido es el conjunto de los números reales positivos.
3) El
valor de y se acerca a cero pero nunca será cero, cuando x toma
valores negativos.
4)
Todas las funciones intersecan al eje y en el punto (0,1).
5) Son
funciones continuas.
Algunas características de las funciones exponenciales decrecientes:
1) El
dominio es el conjunto de los números reales.
2) El
recorrido es el conjunto de los números reales positivos.
3) El
valor de y se acerca a cero pero nunca será cero, cuando x toma
valores positivos.
4)
Todas las funciones intersecan al eje y en el punto (0,1).
5) Son
funciones continuas.
EJERCICIOS:
| x | y = 2x |
|---|---|
| -3 | 1/8 |
| -2 | 1/4 |
| -1 | 1/2 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |


| x | y = 2x |
|---|---|
| -3 | 8 |
| -2 | 4 |
| -1 | 2 |
| 0 | 1 |
| 1 | 1/2 |
| 2 | 1/4 |
| 3 | 1/8 |

Note que para x=0 el valor de f(x) = 1, y para X= 1 el valor de f(x) = 2. Este análisis de constituye en la clave para realizar bosquejos de funciones exponenciales:
Para toda función exponencial no desplazada, la gráfica de la función pasará por 1 siempre que x = 0
Para toda función exponencial no desplazada, la gráfica de la función siempre pasará por el valor de la base. Por ejemplo si la base es 2 como en el ejemplo gráfico, cuando x= 1 la gráfica se ubica exactamente en b= 2

Se puede observar:
Para x = 0, las gráficas pasan por Y = 1; para x = 1, la primera gráfica pasa por Y=4 , y Y= 6 para la segunda gráfica (siendo estos valores las bases de las funciónes exponenciales
Hacer la gráfica de la función exponencial f(x) = 2x
Tabulando para algunos valores cercanos a cero, por ejemplo en el intervalo comprendido entre [-3, 3].
x y
3 2-3 = 0.125
-2 2-2 = 0.25
-1 2-1 = 0.5
0 20 = 1
1 21 = 2
3 32 = 9
Graficando la función exponencial y = 2x:

Dando unos valores a la variable x, se tiene la siguiente tabulación:
x y
-3 (1/2)-3 = 8
-2 (1/2)-2 = 4
-1 (1/2)-1 = 2
0 (1/2)0 = 1
1 (1/2)1 = 0.5
2 (1/2)2 = 0.25
3 (1/2)3 = 0.125
Observaciones:
Para valores de x negativos: cuando x es grande, y tiende a ser grande. Para valores de x positivos, cuando x es grande y tiende a ser muy pequeña.
Graficando la función: y = (1/2)x
Graficando la función: y = (1/2)x

Usando las propiedades de los exponentes, la función y = (1/2)x , se puede escribir como:
y = (1/2)x =
En cierto cultivo habia 500 amebas que se duplicaban por bipartidad cada dia. si ahora hay 256000 ¿ cuantos dias trascurrieron desde que se inicio el cultivo?
Que se "dupliquen" con el paso del tiempo te está indicando que la base de la exponencial es 2 (porque a medida que pasa el tiempo, se multiplica por 2, y la base de la exponencial se multiplica tantas veces como lo dice el exponente). La población inicial es 500, eso significa que el número que tienes que poner multiplicando a exponencial es 500 (¿viste como en el otro era "3", que era cantidad inicial de levaduras presentes?). Y a las variables las podemos llamar "L" (cantidad de levaduras) y "t" tiempo, aclarando que representa al tiempo en "días". La fórmula sería entonces:
L = 500.2t
Luego te pregunta cuántos días (la "t") transcurrieron para que haya 256000 levaduras (la "L"). Así que hay que reemplazar la "L" por 256000, y despejar la "t" para calcular su valor:
L = 500.2t
256000 = 500.2t
Luego, es como los anteriores. Te lo dejo para que practiques. Te digo el resultado: t = 9 días.
Explicación de porqué el valor de la población inicial (500 aquí) se pone multiplicando a la exponencial:
Una función exponencial tiene esta fórmula:
y = k.ax
Para x = 0 (el "tiempo inicial" en estos ejemplos):
y = k.a0y = k.1
y = k
en el momento inicial, la función toma el valor "k": el número que está multiplicando a la exponencial. Si estamos inventando una función exponencial y queremos que su valor en el tiempo inicial sea 500, k debe valer 500. En el ejercicio que vimos:
L = 500.2tL = 500.20L = 500.1
L = 500
Y por qué la base de la exponencial es "2"?
Porque el problema dice que la cantidad de levaduras se "duplica" a medida que pasan los días. Podemos analizar esta situación así:
El día cero: L = 500 (En el instante inicial hay 500 levaduras)
El día "1": L = 500.2 (se duplicó, se multiplicó por "2" la cantidad inicial)
El día "2": L = (500.2).2 (se duplicó la cantidad que había el día anterior)
El día "3": L = (500.2.2).2 (se duplicó la cantidad que había el día anterior)
El día "4": L = (500.2.2.2).2 (se duplicó la cantidad que había el día anterior)
El día "t": L = 500.2t
Analicemos la siguiente función:
En esta gráfica además de hacer una reflexión hacia abajo (todos los valores son negativos), se multiplica por 2, esto provoca una forma diferente de la gráfica. La intersección con el eje "y" es en y = -2; cuando "x" adopta valores muy negativos, el valor de la función tiende a "0", nadamás que en este caso se tiene que acercar por abajo a ese valor, ya que viene de valores siempre negativos.
la función:
Esta función modifica el valor de x, por lo tanto también su apariencia es diferente. Si x = 0, el valor de la función es 2 (1 de la parte exponencial + 1), de ahí en fuera crece más rápido para valores positivos en "x", y decrece más rápido para valores negativos de "x". Otro detalle es, que la función tiene como valor mínimo el 1 (asíntota horizontal en y = 1).
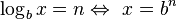
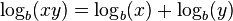
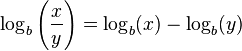
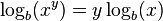
![\!\, \log_b(\sqrt[y]{x}) = \frac{\log_b(x)}{y} \,](http://upload.wikimedia.org/math/e/3/2/e32fd943d2fc67a7033c9d67046522e3.png)
![\!\, \sqrt[y]{x} = x^\frac{1}{y} \,](http://upload.wikimedia.org/math/e/7/d/e7d30a4c68d2e42f12b4fd6bc4417864.png)





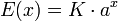



No hay comentarios.:
Publicar un comentario