Función racional
donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo. Las funciones racionales están definidas o tienen su dominio de definición en todos los valores de x que no anulen el denominador.
La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.
Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos.
Propiedades
- Toda función racional es de clase
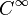 en un dominio que no incluya las raíces del polinomio Q(x).
en un dominio que no incluya las raíces del polinomio Q(x). - Todas las funciones racionales en las que el grado de Q sea mayor o igual que el grado de P tienen asíntotas (verticales, horizontales u oblicuas).
Integración de funciones racionales
Dada una función racional:
Si el denominador es un polinómico mónico
 con k raíces diferentes, entonces admitirá la siguiente factorización en términos de polinomio irreducibles:
con k raíces diferentes, entonces admitirá la siguiente factorización en términos de polinomio irreducibles:Si
 entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas:
entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas:Por lo que la integral de la función
 es una combinación lineal de funciones de la forma
es una combinación lineal de funciones de la forma  :
:Obsérvese que lo anterior implica que las funciones racionales constituyen un cuerpo algebraico que es cerrado bajo la derivación, pero no bajo la intergración.
Asintontas.
Las asíntotas ayudan a la representación de curvas, proporcionan un soporte estructural e indican su comportamiento a largo plazo. En tanto que líneas rectas, la ecuación de una asíntota es simplemente la de una recta, y su expresión analítica dependerá de la elección del sistema de referencias (y = m•x + b en coordenadas cartesianas).
Si bien suelen representarse en un mismo sistema de coordenadas, las asíntotas no forman parte de la expresión analítica de la función, por lo que -en numerosos ejemplos- no están incluidas explícitamente dentro de la gráfica, o bien se las indica con una línea punteada.
En muchos casos, las asíntotas coinciden con los ejes de coordenadas, es decir que sus ecuaciones en coordenadas cartesianas serán: x = 0, y = 0.
Se distinguen tres tipos:
- Asíntotas verticales: rectas perpendiculares al eje de las abscisas, de ecuación x = cte.
- Asíntotas horizontales: rectas perpendiculares al eje de las ordenadas, de ecuación y = cte.
- Asíntotas oblicuas: si no son paralelas o perpendiculares a los ejes, de ecuación y = m•x + b.
EJERCICIOS:
Dejar

El dominio de f es el
conjunto de todos los números reales, excepto 3, desde el 3 de cero hace que el
denominador y la división por cero no está permitido en las matemáticas.
Sin embargo, podemos
tratar de averiguar cómo la gráfica de f se comporta cerca de
3.
Vamos a evaluar la
función f en los valores de x cerca de 3 tal que x <3. Los valores se muestran en la tabla
siguiente:
| x | 1 | 2 | 2,5 | 2,8 | 2,9 | 2,99 | 2,999 | 2,99999 |
| f (x) | -1 | -2 | -4 | -10 | -20 | -200 | -2000 | -2 * 10 5 |
| x | 5 | 4 | 3,5 | 3,2 | 3,1 | 3,01 | 3,001 | 3,00001 |
| f (x) | 1 | 2. | 4 | 10 | 20 | 200 | 2000 | 2 * 10 5 |

Horizontal
asíntotas
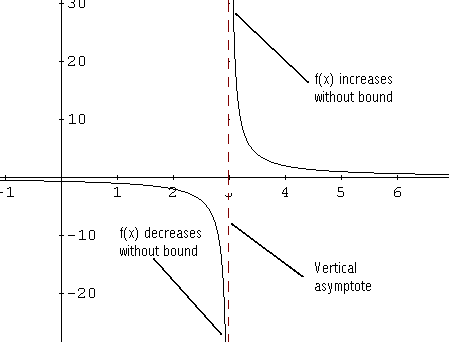
Dejar

1 - Sea x aumento y
encontrar los valores de f (x).
| x | 1 | 10 | 10 3 | 10 6 |
| f (x) | 3 | 2.1 | 2,001 | 2,000001 |
2 - Sea x disminución y
encontrar los valores de f (x).
| x | -1 | -10 | -10 3 | -10 6 |
| f (x) | 1 | 1,9 | 1,999 | 1,999999 |
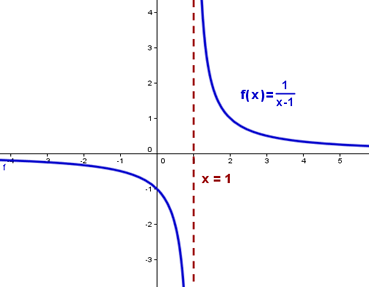
Sea f una función racional definida por

a - Encontrar el dominio
de f.
Encuentra la x , y
intercepta de la gráfica de f.
c - Encuentre las
asíntotas vertical y horizontal para la gráfica de f si los
hay.
d - Utiliza tus
respuestas a las partes a, b y c por encima de para trazar la gráfica de la
función f.
Respuesta a la
Ejemplo 1
a - El dominio de f es
el conjunto de todos los números reales excepto x = 1, ya que este valor de x
cero hace que el denominador.
b - La x intercepte se
encuentra por la solución de f (x) = 0 ó x +1 = 0. x La intersección está en el punto (-1,
0).
La intersección está en
el punto (0, f (0)) = (0, -1).
c - La asíntota vertical
está dada por el cero en el denominador x = 1.
El grado del numerador
es 1 y el grado del denominador es 1. Son iguales y de acuerdo con el teorema anterior, la
asíntota horizontal es la recta y = 1 / 1 = 1
e - Aunque las partes a,
b y c dan información importante sobre la gráfica de f, todavía tenemos que
construir una tabla de señal para la función f con el fin de ser capaz de
dibujar con facilidad.
El signo de f (x) los
cambios en los ceros del numerador y el denominador. Para encontrar la tabla de signo, se procede como en
la solución de las desigualdades racionales. Los ceros del numerador y el denominador que son -1
y 1 divide la línea número real en 3 intervalos:
(- Infinito, -1), (-1,
1), (1, + infinito).
Hemos seleccionado un
valor de prueba dentro de cada intervalo y encontrar el signo de f
(x).
En (- infinito, -1), -2
seleccionar y encontrar f (-2) = (-2 + 1) / (-2 - 1) = 1 / 3>
0.
En (-1, 1), 0
seleccionar y encontrar f (0) = -1 <0.
En (1, + infinito), 2
seleccionar y encontrar f (2) = (2 + 1) / (2 - 1) = 3>
0.
Vamos a poner toda la
información acerca de f en una tabla.
| x |
- Inf
|
-1 | 1 |
+ Inf
| |
| f (x) | + | 0
x-intercepta |
-- | AV | + |
En el cuadro anterior significa VA
asíntota vertical.
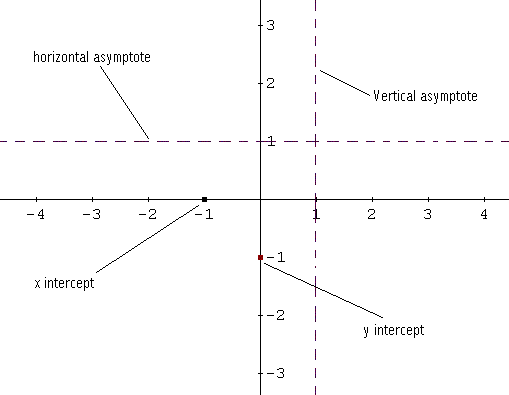
Para dibujar la gráfica de f, se comienza
por esbozar el X e intercepta y y las asíntotas verticales y horizontales en las
líneas rotas. Véase el croquis.
Ahora empezar a dibujar la gráfica de f a
partir de la izquierda.
En el intervalo de inf (-, -1) f (x) es
positiva por lo tanto, el gráfico está por encima del eje x. Comenzando desde la izquierda dibujo, que f teniendo en
cuenta el hecho de que y = 1 es una asíntota horizontal: la gráfica de f está
cerca de la línea de la izquierda. Véase el croquis.

Entre -1 y 1, f (x) es negativa, por lo
tanto, la gráfica de f está por debajo del eje x. (0, -1 intersección) es ay y x
= 1 es una asíntota vertical: cuando x se aproxima a 1 de izquierda f (x)
Difuntos sin límite porque f (x) <0 en (-1, 1). Véase el croquis.
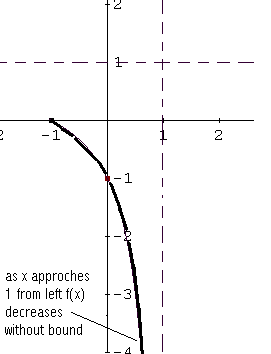
Para x> 1, f (x)> 0 por lo tanto,
el gráfico está por encima del eje x. Cuando x
se aproxima a 1 por la derecha, la gráfica de f aumenta sin límite (f (x)>
0). También a medida que aumenta x, la gráfica
de f enfoques y = 1, la asíntota horizontal. Véase el croquis.
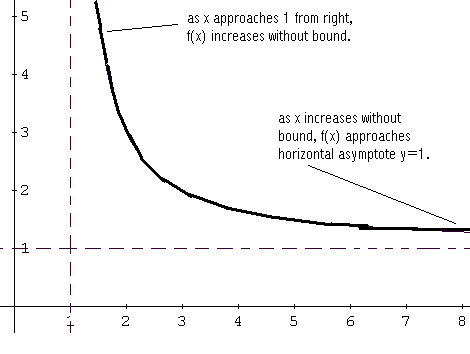
Ahora ponemos todas las "piezas" de la
gráfica de f en conjunto para obtener la gráfica de f.

Dibuja la gráfica de la función

Lo primero es hacer la división:

Luego:

La hipérbola que tengo que representar es la misma que
 desplazada horizontalmente 3 unidades a la izquierda y 2 hacia arriba:
desplazada horizontalmente 3 unidades a la izquierda y 2 hacia arriba:
- La función
tiene una asíntota vertical en x=2, aunque existe f(2).
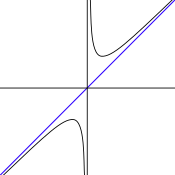
f(x), en x=1 presenta una asíntota vertical, ya que la función se aproxima cada vez más a la recta vertical x=1 cuando x tiende a 1.
.

El centro de la hipérbola es: (0, 3)
Si a<0,  se desplaza hacia abajo a unidades.
se desplaza hacia abajo a unidades.



El centro de la hipérbola es: (-1, 3)

El centro de la hipérbola es: (-3, 0)




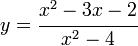
![f(x) = \frac{P(x)}{Q(x)}, \qquad P(x),Q(x)\in \R[x]](http://upload.wikimedia.org/math/8/e/4/8e418aac8dbe42c60615386abe8a0d10.png)




 y n es un entero no negativo.
Entonces, f se llama una Función Polinomial de grado n.
y n es un entero no negativo.
Entonces, f se llama una Función Polinomial de grado n.


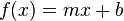









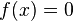 . Por tratarse de un polinomio de grado 2, habrá a lo sumo 2 raíces, denotadas habitualmente como:
. Por tratarse de un polinomio de grado 2, habrá a lo sumo 2 raíces, denotadas habitualmente como:  y
y  , dependiendo del valor del
, dependiendo del valor del  .
.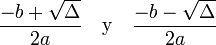 .
.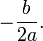
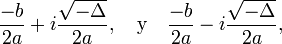
 .
.
 . En el caso de que el
. En el caso de que el  por lo que la factorización adquiere la forma:
por lo que la factorización adquiere la forma:



















