FUNCIÓN POLINOMIAL DE GRADO CERO
Definición Si una función f está definida por
f(x) = anXn + an1 − 1Xn − 1 + an − 2Xn − 2 + ... + a1 + a0 donde a0,a1,...,an son números reales  y n es un entero no negativo.
Entonces, f se llama una Función Polinomial de grado n.
y n es un entero no negativo.
Entonces, f se llama una Función Polinomial de grado n.
La gráfica de una función polinomial de grado 0, que es de la forma f(x) = a


y= 8, y = 4.2, y= -3.6,
FUNCIÓN LINEAL
Algunos autores llaman función lineal a aquella con b= 0 de la forma:
Grafique la ecuación x + 2y = 7.
Puede encontrar dos soluciones, correspondientes a la intercepción en x y a la intercepción en y de la gráfica, colocando primero x = 0 y luego y = 0.
Cuando x = 0, obtenemos:
0 + 2y = 7
y = 3.5
Cuando y = 0, obtenemos:
x + 2(0) = 7
x = 7
Así los dos puntos son (0, 3.5) y (7, 0).
Grafique estos dos puntos y dibuje la recta que los une.

Puede encontrar dos soluciones, correspondientes a la intercepción en x y a la intercepción en y de la gráfica, colocando primero x = 0 y luego y = 0.
Cuando x = 0, obtenemos:
0 + 2y = 7
y = 3.5
Cuando y = 0, obtenemos:
x + 2(0) = 7
x = 7
Así los dos puntos son (0, 3.5) y (7, 0).
Grafique estos dos puntos y dibuje la recta que los une.

Grafique la recta y = 3x + 1.
De la ecuación, sabemos que la intercepción en y es 1, el punto (0, 1) y la pendiente es 3. Grafique el punto (0, 1) y desde ahí suba 3 unidades y luego a la derecha 1 unidad y grafique un segundo punto. Dibuje la recta que contiene ambos puntos.

Las rectas horizontales y verticales tienen ecuaciones de primer grado sencillas.
De la ecuación, sabemos que la intercepción en y es 1, el punto (0, 1) y la pendiente es 3. Grafique el punto (0, 1) y desde ahí suba 3 unidades y luego a la derecha 1 unidad y grafique un segundo punto. Dibuje la recta que contiene ambos puntos.

Las rectas horizontales y verticales tienen ecuaciones de primer grado sencillas.
Recta horizontal: y = 3
Recta vertical: x = –2

Recta vertical: x = –2

El precio de una television es de $200.00 al contado, pero si se compra en abonos se cobra un interés mensual fijo de $10.00.
a) ¿Cuánto debe pagarse si se compra al contado o en plazos de 1,2,3,4,5 ó 6 meses?
b) Tabula y construye la gráfica.
c) Anota la expresión algebraica que determina la regla de correspondencia de la
función.
RESULTADO
a) Al comprarlo en abonos se tendrá que pagar:

a) ¿Cuánto debe pagarse si se compra al contado o en plazos de 1,2,3,4,5 ó 6 meses?
b) Tabula y construye la gráfica.
c) Anota la expresión algebraica que determina la regla de correspondencia de la
función.
RESULTADO
a) Al comprarlo en abonos se tendrá que pagar:
A un mes 200 + 10 ( 1 ) = 210 dos meses 200 + 10 ( 2 ) = 220 tres meses 200 + 10 ( 3 ) = 230 cuatro meses 200 + 10 ( 4 ) = 240 cinco meses 200 + 10 ( 5 ) = 250 seis meses 200 + 10 ( 6 ) = 260
b ) Los datos anteriores nos dan la tabla y la gráfica siguiente:
| x | y = f (x) |
|---|---|
| 0 | 200 |
| 1 | 210 |
| 2 | 220 |
| 3 | 230 |
| 4 | 240 |
| 5 | 250 |
| 6 | 260 |

Gráfica
c) Por lo tanto, la cantidad que debe pagarse en un plazo de x meses es: f (x) = 200 +10x
la cual es la expresión algebraica que determina esta función.
40
meses?
b) Tabula y construye la gráfica.
c) Encuentra la expresión algebraica que determine la función que describe al problema. SOLUCIÓN:
a) Tendremos que designar una incógnita que represente el número de meses, que en
nuestro ejemplo será x.
Entonces: Para cero meses, Patricia pagará $500.00 + 10(0) = $500.
Para un mes, $500.00 + 10(1) = $510.
Para dos meses, $500.00 + 10(2) = $520.
Para tres meses, $500.00 + 10(3) = $530.
¿Cuánto deberá pagar los meses restantes del plazo?.
b) Si tabulas los datos anteriores tendrás la siguiente tabla:
| x | y |
|---|---|
| 0 | 500 |
| 1 | 510 |
| 2 | 520 |
| 3 | 530 |
| 4 | 540 |
| 5 | 550 |
| 6 | 560 |
41
Por lo tanto, la gráfica es: 
c) Con base en la proposición del inciso a) podemos establecer la expresión solicitada, que es:
f (x) = 10x + 500
FUNCIÓN CUADRATICA

en donde a, b y c son números reales (constantes) y a es distinto de 0.
La representación gráfica en el plano cartesiano de una función cuadrática es una parábola, cuyo eje de simetría es paralelo al eje de las ordenadas. La parábola se abrirá hacia arriba si el signo de a es positivo, y hacia abajo en caso contrario. El estudio de las funciones cuadráticas tiene numerosas aplicaciones en campos muy diversos, como por ejemplo la caída libre o el tiro parabólico.
La derivada de una función cuadrática es una función lineal y su integral una función cúbica.
Las raíces (o ceros) de una función cuadrática, como en toda función, son los valores de x, para los cuales 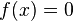 . Por tratarse de un polinomio de grado 2, habrá a lo sumo 2 raíces, denotadas habitualmente como:
. Por tratarse de un polinomio de grado 2, habrá a lo sumo 2 raíces, denotadas habitualmente como:  y
y  , dependiendo del valor del discriminante Δ definido como
, dependiendo del valor del discriminante Δ definido como  .
.
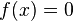 . Por tratarse de un polinomio de grado 2, habrá a lo sumo 2 raíces, denotadas habitualmente como:
. Por tratarse de un polinomio de grado 2, habrá a lo sumo 2 raíces, denotadas habitualmente como:  y
y  , dependiendo del valor del discriminante Δ definido como
, dependiendo del valor del discriminante Δ definido como  .
.- Dos soluciones reales y diferentes si el discriminante es positivo:
-
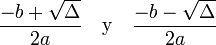 .
.
- Una solución real doble si el discriminante es cero:
- Dos números complejos conjugados si el discriminante es negativo:
Forma desarrollada
La forma desarrollada de una función cuadrática (o forma estándar) corresponde a la del polinomio de segundo grado, escrito convencionalmente como:
 .
.Forma factorizada
Toda función cuadrática se puede escribir en forma factorizada en función de sus raíces como: y
y  las raíces de
las raíces de  . En el caso de que el discriminante Δ sea igual a 0 entonces
. En el caso de que el discriminante Δ sea igual a 0 entonces  por lo que la factorización adquiere la forma:
por lo que la factorización adquiere la forma: se la denomina raíz doble, ya que su orden de multiplicidad es 2.
se la denomina raíz doble, ya que su orden de multiplicidad es 2.Forma canónica
Toda función cuadrática puede ser expresada mediante el cuadrado de un binomio de la siguiente manera:EJERCICIOS:
- El ánimo de lucro (en miles de dólares) de una empresa está dada por.
donde x es la cantidad (en miles de dólares) que la empresa gasta en
publicidad.
- Encuentre la cantidad, x, que la empresa tiene que
pasar para maximizar su beneficio.
- Encuentra el máximo beneficio Pmax.
Solución del Problema 1:
- P Función que le da el
beneficio es una función cuadrática con el coeficiente líder de -5 =.
Esta función (sin
fines de lucro) tiene un valor máximo en x = h = -b/2a x = H = -1000 / 2 (-5) = 100
- La ganancia máxima Pmax, cuando
x = 100 miles se gasta en publicidad, está dada por el valor máximo de la
función P k = c - b 2 / 4a
- La ganancia máxima Pmax, cuando
x = 100 miles se gasta en la publicidad, también está dada por P (h =
100) P (100) = 5000 + 1000 (100) - 5 (100) 2 = 55000.
- Cuando la empresa gasta 100 mil
dólares en publicidad, el beneficio es máximo y es igual a 55.000
dólares.
- Abajo se muestra la gráfica de
P (x), observe el punto máximo, el vértice, en (100, 55000).

La parábola "básica", y = x2, se ve así:


Encuentre el vértice de la parábola.
y = 3x2 + 12x – 12
Aquí, a = 3 y b = 12. Así, la coordenada en x del vértice es:

Sustituyendo en la ecuación original para obtener la coordenada en y, obtenemos:
y = 3(–2)2 + 12(–2) – 12
= –24
Así, el vértice de la parábola está en (–2, –24).
y = 3x2 + 12x – 12
Aquí, a = 3 y b = 12. Así, la coordenada en x del vértice es:

Sustituyendo en la ecuación original para obtener la coordenada en y, obtenemos:
y = 3(–2)2 + 12(–2) – 12
= –24
Así, el vértice de la parábola está en (–2, –24).
El eje de simetría de una parábola es la recta vertical a través del vértice. Para una parábola en la forma estándar, y = ax2 + bx + c, el eje de simetría tiene la ecuación

Dese cuenta que –b/2a también es la coordenada en x del vértice de la parábola.
Ejemplo:
y = 2x2 + x – 1


Considera la función f(x) = x2 - 4
Otro
ejemplo que podemos mencionar es en f(x) = x2 + 2x – 3 = (x + 3)(x –
1) donde x = -3 y x = 1 son las soluciones o
raíces.
La función cuadrática más sencilla es f(x) = x2 cuya gráfica es:
| x | -3 | -2 | -1 | -0'5 | 0 | 0'5 | 1 | 2 | 3 |
| f(x) = x2 | 9 | 4 | 1 | 0'25 | 0 | 0'25 | 1 | 4 | 9 |

Funciones cuadráticas más complejas se dibujan de la misma forma.
Dibujemos la gráfica de f(x) = x2 -2 x - 3.
x -1 0 1 2 3 4 f(x) 0 -3 -4 -3 0 5
Completando la gráfica obtengo:
- Dada la parábola y = x2 - 4 x + 3, determina con precisión las coordenadas de los puntos de la f:

- a. Del punto A(x,y) conocemos que x = 3'5. Como A es un punto de la parábola, sus coordenadas cumplirán la ecuación, es decir, y = 3'5 2 - 4·3'5 + 3 = 1'25. Por tanto, A = (3'5,1'25).
- b. Del punto B(x,y) conocemos que x = 7. Como B no pertenece a la parábola, no disponemos de ninguna relación que nos permita deducir y en función de x: no es posible conocer con precisión las coordenadas de B.
- c. El punto C(x,y) está situado sobre el eje de ordenadas, luego x = 0. Como también es un punto de la parábola, verificará y = 02 - 4·0 + 3 = 3 .Luego C = (0,3).
- d. D = (x,5) pertenece a la parábola. Sustituyendo y por 5 en la ecuación de la parábola:
 , que nos proporciona las soluciones aproximadas x = -0'45 y x = 4'45 . Observando la gráfica se concluye que el valor adecuado es el segundo (¿por qué?). Luego D = (4'45,5).
, que nos proporciona las soluciones aproximadas x = -0'45 y x = 4'45 . Observando la gráfica se concluye que el valor adecuado es el segundo (¿por qué?). Luego D = (4'45,5).- e. Los puntos E y F pertenecen al eje OX . Sus coordenadas serán de la forma (x,0) y por ser de la parábola verificarán la ecuación de 2º grado x2 - 4x + 3 = 0 , cuyas soluciones son x = 1 y x = 3. Por tanto, los puntos serán E = (1,0) y F = (3,0).
- f. Por la forma simétrica de la parábola, la abscisa de G = (x,y) es el punto medio del segmento
 , es decir,
, es decir,  . Sustituyendo este valor en la ecuación de la parábola, obtenemos su segunda coordenada y = 22 - 4·2 + 3 = 4 - 8 + 3 = -1. Luego G = (2,-1).
. Sustituyendo este valor en la ecuación de la parábola, obtenemos su segunda coordenada y = 22 - 4·2 + 3 = 4 - 8 + 3 = -1. Luego G = (2,-1). - g. Calculemos las coordenadas del punto H´(x,y) de la parábola que está "justo encima" de H.
- Como x = 5, entonces y = 52 - 4·5 + 3 = 25 - 20 + 3 = 8 , es decir, H´= (5,8). H tiene igual abscisa 5 y su ordenada es 6 unidades menos que H´, por tanto, H = (5,2).
- h. Calculamos las coordenadas del punto I´(x,7) que está en la parábola "justo a la derecha" de I. Como pertenece a la parábola ,
 cuyas soluciones aproximadas son x = -0'88 y x = 4'83. I tiene la misma ordenada 7 y su abscisa es 4'2 unidades menos que la abscisa de I´, es decir, I = (0'63,7).
cuyas soluciones aproximadas son x = -0'88 y x = 4'83. I tiene la misma ordenada 7 y su abscisa es 4'2 unidades menos que la abscisa de I´, es decir, I = (0'63,7).
- Determina, por este orden, las coordenadas de los puntos A, B, el vértice V y el punto C de la parábolay = x2 - x + 1 .
 a. A está situado en el eje Y, es decir sus coordenadas son de la forma A(0,y). Puesto que A pertenece a la parábola, y = 02- 0 + 1, y = 1. Luego A = (0,1).b. B ha de ser de la forma (x,1), por tanto, 1 = x2 - x + 1; 0 = x2- x, 0 = x · (x - 1) de soluciones x = 0 y x = 1. Luego B = (1,1).c. La 1ª coordenada del vértice está situada en el punto medio del segmento de extremos 0 y 1, es decir,
a. A está situado en el eje Y, es decir sus coordenadas son de la forma A(0,y). Puesto que A pertenece a la parábola, y = 02- 0 + 1, y = 1. Luego A = (0,1).b. B ha de ser de la forma (x,1), por tanto, 1 = x2 - x + 1; 0 = x2- x, 0 = x · (x - 1) de soluciones x = 0 y x = 1. Luego B = (1,1).c. La 1ª coordenada del vértice está situada en el punto medio del segmento de extremos 0 y 1, es decir, . La 2ª coordenada se obtiene con la ecuación y = (0'5)2- 0'5 + 1 = 0'75. Las coordenadas del vértice serán V = (0'5,0'75).d. Utilizando la simetría de la parábola puedo calcular la 1ª coordenada de C, x = 2. Por lo tanto,y = 22-2+1=3. C = (2,3).Este método se puede generalizar a cualquier parábola de ecuación y = ax2 + bx + c y nos permitirá hallar el vértice de forma inmediata.Obtención general del vértice
. La 2ª coordenada se obtiene con la ecuación y = (0'5)2- 0'5 + 1 = 0'75. Las coordenadas del vértice serán V = (0'5,0'75).d. Utilizando la simetría de la parábola puedo calcular la 1ª coordenada de C, x = 2. Por lo tanto,y = 22-2+1=3. C = (2,3).Este método se puede generalizar a cualquier parábola de ecuación y = ax2 + bx + c y nos permitirá hallar el vértice de forma inmediata.Obtención general del vértice Sea la parábola y = ax2 + bx + cLocalizado el corte con el eje Y, (0,c) hallamos su simétrico resolviendo el sistema
Sea la parábola y = ax2 + bx + cLocalizado el corte con el eje Y, (0,c) hallamos su simétrico resolviendo el sistema .Igualando:a x2 + b x + c = c → a x2 + b x = 0 → x (a x + b) = 0; es decir, x = 0 ó ax + b = 0 que nos lleva a la solución x = -b/a.
.Igualando:a x2 + b x + c = c → a x2 + b x = 0 → x (a x + b) = 0; es decir, x = 0 ó ax + b = 0 que nos lleva a la solución x = -b/a.
- Dibuja la gráfica de y = 4x2 + 4x + 1.Como a = 4 es positivo la parábola tiene sus ramas hacia arriba.La 1ª coordenada del vértice es p = -b/(2a) = -4/2·4 = -0'5.Y la 2ª coordenada q = 4·(-0'5)2 + 4(-0'5) + 1 = 0. Luego el vértice es V(-0'5,0).Utilizando valores de x situados a la misma distancia de -0'5 por la izquierda y por la derecha:


- Dibuja la gráfica de
 Como a = -1/2 es negativo, la parábola tiene sus ramas hacia abajo.La 1ª coordenada del vértice es
Como a = -1/2 es negativo, la parábola tiene sus ramas hacia abajo.La 1ª coordenada del vértice es La segunda coordenada será:
La segunda coordenada será: .El vértice es, pues, V(2,-1)Utilizando valores de x situados a la misma distancia de 2 por la izquierda y por la derecha:
.El vértice es, pues, V(2,-1)Utilizando valores de x situados a la misma distancia de 2 por la izquierda y por la derecha:

y = x2 - 2x + 3

Puntos de corte con el eje X:
Si resolvemos la ecuación x2 - 2x + 3 = 0
obtenemos que  . No existe solución y, por lo tanto, no tiene
cortes con el eje X.
. No existe solución y, por lo tanto, no tiene
cortes con el eje X.
Punto de corte con el eje Y: (0,3)
y = - x2 + 2x + 3

Los puntos de corte con el eje X son de la forma (x,0).
Sustituyendo y por 0 en la fórmula obtenemos la ecuación de 2º grado -
x2 + 2x + 3 = 0
,
cuyas soluciones son x = -1, y x = 3.
Los puntos de corte son (-1,0),
(3,0).
El punto de corte con el
eje Y se obtiene haciendo x = 0 en la ecuación de la parábola. Por tanto, será
(0,3).


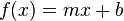



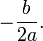
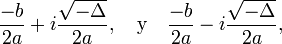




No hay comentarios.:
Publicar un comentario