FUNCIÓN.

La definición general de función hace referencia a la dependencia entre los elementos de dos

conjuntos dados.

Dados dos conjuntos B, una función (también aplicación o mapeo) entre ellos es una asociaciónf que a cada elemento de A le asigna un único elemento de B.
Se dice entonces que A es el dominio (también conjunto de partida o conjunto inicial) de f y que B es su codominio (también conjunto de llegada o conjunto final).

La función es una relación que se puede representar de varias formas puede ser :

SAGITAL: Representación de dos elementos conjuntos de elementos empleando flechas.

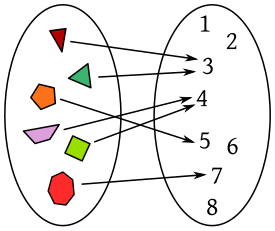
Parejas ordenadas: Decribe los puntos P ( x , y ).

( 0 , 0 ) ( 1 , 1 ) ( 2 , 4) ( 3 , 9)

Analitica : Modelo matematicoque muestra dos variables.

y= k²

Criterio de la recta vertical

No toda curva es la grafica de una función, existe una regla de geométrica que nos permite saber si una grafica es una función o simplemente una relación.

" Una curva es la grafica de una función si y solo si al trazar rectas verticales sobre ella, ninguna de ellas la intercepta en más de un solo punto a la vez"

la recta vertical)

Así por ejemplo, la gráfica de la figura 1(a) corresponde a la gráfica de una función (la recta vertical solo corta la gráfica en el punto A); mientras que la figura 1(b) no corresponde a la gráfica de una función. Nótese que la recta vertical, corta la gráfica en mas de un punto: A, B y C.

REGLA DE CORRESPONDENCIA

Denominamos como (Regla de correspondencia) al hecho de asignar a cada elemento cualesquiera otro elemento único dado cualesquiera.

Dicho en otras palabras, es el proceso que víncula a cada elemento de un conjunto determinado con otro elemento único de otro conjunto determinado… Donde dichos conjuntos pueden ser el (Dominio y Codominio) de una función.

DOMINIO Y CONTRADOMINIO.

El dominio de definición de una función f:X→Y se define como el conjuntode todos los elementos x para los cuales la función f asocia algún y perteneciente al conjunto Y de llegada, llamado codominio. Esto, escrito de manera formal:

$D_f = \; \left\{x \in X | \exists y \in Y: f(x)=y\right\}$

El contradominio son todos los valores que se pueden en una variable dependiente y que generalmente se representa con una Y a los cuales manda la función cuando aplicas la regla de correspondencia.

Algunos dominios de funciones reales de variable real:

$f(x)=x^2 \,\!$ El dominio de esta función es $\mathbb{R}$ .

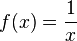$f(x)= \frac{1}{x}$ El dominio de esta función es $\mathbb{R}-\lbrace0\rbrace$ puesto que la función no está definida para x = 0.

$f(x)= \log(x) \,\!$ El dominio de esta función es $(0,{+}\infty)$ ya que los logaritmos están definidos sólo para números positivos.

$f(x)= \sqrt{x}$ El dominio de esta función es $\lbrack0,{+}\infty)$ porque la raíz de un número negativo no existe en el cuerpo de los re

SIMBOLOGIA PARA INTERVALOS

EJERCICIOS:

¿Cuál es el dominio de la funcion f (x)

3 x2- Sx - 6

Solución: Lafunción es polinomial, "x" puede tomar cualquier valor, por lo tanto el dominio son todos los números

reales, es decir x e R o dicho de otra/orma x e (-00,00) .

Determina el dominio de la funcion f ( x ) = x -3 / x+5

La función es racional, el denominador debe ser distinto de cero, ya que la división entre cero no esta

definida, por lo tanto, se busca el valor para el cual x + 5 = 0 obteniendo x - 5, por lo tanto el dominio es de

es:D¡= {xeR / x = -5} o bien x e (-oo,-5)u(-5,oo)

Determina el domninio de la función f (x) = X / x²- 5x -6

al factorizar se obtiene f (x) = x / ( x - 6) ( x - 1 ) el denominador se hace 0 para x= 6 o x = -1

DI= {x e R I x = -l,x = 6} o bien x e (-00,-1) u(-1,6) u (6,00).

Determina el dominio de f (x) = RAIZ DE x - 5

El radicando debe ser igual o mayor a 0 es decir x -5 > 0 de donde x > 5 por lo tanto

DI= {xeRlx=5}

Determina el dominio de f (x) = log (2x-3)

Para determinar el ddominio de esta función se debe tomar en cuenta que si log N= a, entonces N > 0 por lo tanto se plantea la desigualdad y se resuelve

2x-3>0-72x>3-7x> - 2/3

D I= {x e R IX>~} o bien x e (~,oo)

Si f (x) = 1 / x +2

El Dom(f) está dado por el conjunto de los valores de x para los que f(x)

existe. Esta función no tiene sentido cuando el denominador es cero.

Dicho de otro modo, la función existe para todos los valores de x para los

que el denominador es distinto de cero.

Dom(f)

= ∀x ∈ ℝ/x+2 ≠0⇒Dom(f)= ∀x ∈ ℝ/x≠−2

DOMINIO CONTRADOMINIO

Y = X+1 { XER} { Y/YER, Y>0}

f (x)= 1/x+2 {x/ER; X=-2} {Y/YER;Y=0}

G(x)= 2x² - 4x-30/ x+3 { x/ xER; X= -3} { y/YER ;y= -16}

Encontrar el dominio de la función siguiente: h (x)= x²+ 5 / x-1

Cuando x = 1 el denominador de la función es cero. Pero cuando x

≠ 1 el

denominador es siempre un número real. Por lo tanto el dominio de la función h

consiste de todos los números reales

excepto el 1. Esto se puede escribir de las

siguientes dos maneras (1) D(-∞, 1)∪(1, +∞).

OPERACIONES CON FUNCIÓNES.

Al igual que las operaciones con números, las funciones se pueden sumar, restar, multiplicar y dividir.

Sean f ( x) y g ( x) podemos efectuar las siguientes operaciónes:

Si f (x) = 2x + 1y h (x) = |x| entonces:

( h + f )(x) = h (x) + f (x) = |x| + 2x + 1

( h + f )(2) = h (2) + f (2) = |2| + 2 ( 2 ) + 1= 7

Si f (x) = 2x + 1, g (x) = x²entonces:

( f - g )( x ) = f (x) - g (x) = 2x + 1 - x² = 1 + 2x - x²

( f - g )(- 1) = f (- 1) - g (- 1) = 2 ( -1) + 1 - ( -1)² = -2 + 1 - 1 = - 2

Si g (x) = x²y h (x) = x - 2 entonces:

( h • g )(x) = h (x) • g (x) =( x - 2 ) x² = x³ – 2x²

( h • g )(5) = h (5) • g (5) = ( 5 - 2 ) ( 5 )² = 3 (25) = 75

f (x) = x ² - 3, y g(x) = x + 3, definir la función (f - g)(x).

Calcular las imágenes de 1/3, -2 y 0 mediante la función f - g.

Resolución:

- (f - g)(x) = f(x) - g(x) = x ² - 3 - (x + 3) = x ² - 3 - x - 3 = x ² - x - 6

- (f - g)(1/3) = (1/3) ² - 1/3 - 6 = - 56/9

- (f - g)(-2) = (-2) ² - (-2) - 6 = - 0

- (f - g)(0) = (0) ² - 0 - 6 = - 6

Si f(x) = 4x y g(x) = x² – 4x +3 efectuar las siguientes operaciónes

f(x) + g (x)= ( f +g) (x) = 4x + ( x² – 4x +3)
                                       = x²+3

f(x) * g(x) = ( f *g)(x) = 4x ( x² – 4x +3)
                                      = 4

f(x) - g(x) = ( f - g) ( x ) = 4x -( x² – 4x +3)
                                         = 4x - x² + 4x -3)
                                          = - x² + 8x - 3

CLASIFICACIÓN DE FUNCIONES.

FUNCIÓN RACIONAL: una función racional es una función que puede ser expresada de la forma:

$f(x) = \frac{P(x)}{Q(x)}$

donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo. Las funciones racionales están definidas o tienen su dominio de definición en todos los valores de x que no anulen el denominador.
La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.
Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos.

$y = \cfrac{x^2 -3x -2}{x^2 -4}$

FUNCIÓN IRRACIONAL:

Las funciones irracionales son aquellas cuya expresión matemática f(x) presenta un radical,
Las características generales de estas funciones son:
a) Si el índice del radical es par, el dominio son los valores para los que el radicando es mayor o igual que cero.
b) Si el índice del radical es impar, el dominio del radicando es negativo o menor que cero.
c) Es continua en su dominio y no tiene asíntotas.

FUNCIÓN TRIGONOMETRICA DIRECTA: Son aquellas que tienen: seno, coseno. tangente, cotangente, cosecante, cotangente

f (x) = 2sen(3x)
f (k) = -cos(4k )
f ( t) = tan ( 2t)

FUNCIÓN TRIGONOMETRICA INVERSA: Son de la siguiente forma arco seno, arco coseco,

f(x)= arc sen ( x )
g (x) = arc tan (x)

FUNCIÓNES EXPONENCIALES: es conocida formalmente como la función real e^x, donde e es el número de Euler, aproximadamente 2.71828...; esta función tiene por dominio de definicióN el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=e^x o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.
En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma

$E(x)=K \cdot a^x$

siendo a, K ∈ R números reales, con a > 0. Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base a que utilicen

FUNCIÓN LOGARITMICA:
Dado un número real (argumento x), la función logaritmo le asigna el exponente n (o potencia) a la que un número fijo b (base) se ha de elevar para obtener dicho argumento. Es la función inversa de b a la potencia n. Esta función se escribe como: n = log_b x, lo que permite obtener n.

$\log_b x = n\Leftrightarrow\ x = b^n\,$

(esto se lee como: logaritmo en base b de x es igual a n; si y sólo si b elevado a la n da por resultado a x)
Para que la definición sea válida, no todas las bases y números son posibles. La base b tiene que ser positiva y distinta de 1, luego b> 0 y b ≠ 1, x tiene que ser un número positivo x > 0 y n puede ser cualquier número real (n ∈ R).
Así, en la expresión 10² = 100, el logaritmo de 100 en base 10 es 2, y se escribe como log₁₀ 100 = 2.

EJERCICIOS:

f(x) = arccosen x

Dominio: [-1, 1]

Continua: (-1, 1)

Decreciente: (-1, 1)

Resolver

Resolución:

Un cultivo de bacterias, con un numero inicial de 1000 bacterias, dobla su tamaño cada hora. Encuentra una formula para el numero N(t) de bacterias presentes despúes de t horas. Cuantas bacterias estaran presentes después de 8 horas.

SOLUCIÓN: N(8)= 1000(28)
= 256 000

RESOLVER:

2^{x²- 1}= 8

2^{x²- 1}= 2³x²- 1= 3

x²= 3 + 1

x = 2; x = - 2

5^{x + 3}= 25
5^{x + 3}= 5²x + 3 = 2

x = - 1

9^{x + 1} + 3^{x + 2}- 810 = 0

3^{2(x + 1)} + 3^{x + 2} - 810 = 0;

Si sustituimos 3^x por p; resulta
9p² + 9p - 810 = 0;
p² + p - 90 = 0; p = - 10; p = 9;

sus tituyendo este valor en 3^x, resulta:
3^x= - 10;
3^x= 9; 3^x = 3²

x = 2

f es una función dada por

f (x) = log ₂ (x + 2)

Determine el dominio de f y el rango de f.
Encuentra la asíntota vertical de la gráfica de f.
Encuentra la X y la intercepta y de la gráfica de f si los hay.
Dibuje la gráfica de f.

a - El dominio de f es el conjunto de todos los valores de x tal que

x + 2 > 0

x > -2

El rango de f es el intervalo (-inf, + inf).

b - La asíntota vertical se obtiene mediante la solución de

x + 2 = 0

lo que da

x = -2

Cuando x tiende a -2 de la derecha (x> -2), f (x) decrece sin límite. ¿Cómo sabemos esto?

Veamos algunos valores:

f (-1) = log ₂ (-1 + 2) = log ₂ (1) = 0

f (-1,5) = log ₂ (-1,5 + 2) = log ₂ (1 / 2) = -1

f (-1,99) = log ₂ (-1,99 + 2) = log ₂ (0.01), que es aproximadamente igual a -6,64

f (-1.999999) = log ₂ (-1,999999 + 2) = log ₂ (0.000001), que es aproximadamente igual a -19,93.

c - Para encontrar la intersección x tenemos que resolver la ecuación f (x) = 0

log₂ (x + 2) = 0

Usar las propiedades de las funciones logarítmicas y exponenciales para escribir la ecuación anterior como

x + 2 = 2^0

x = -1

La intersección x es (-1, 0).

La intersección está dada por (0, f (0)) = (0, log ₂ (0 + 2)) = (0, 1).

d - Hasta ahora tenemos el dominio, rango, x e intercepta y, y la asíntota vertical. Necesitamos más puntos. Vamos a considerar un punto en x = -3 / 2 (a medio camino entre la X y la intersección de la asíntota vertical) y otro punto en x = 2.

f (-3 / 2) = log ₂ (-3 / 2 + 2) = log ₂ (1 / 2) = log ₂ (2 ^-1) = -1.

f (2) = log ₂ (2 + 2) = log ₂ (2 ²) = 2.

Ahora tenemos más información sobre la forma de gráfico de f. El gráfico aumenta a medida que aumenta x. Cerca de la asíntota vertical x = -2, la gráfica de f disminuye sin límite cuando x tiende a -2 de la derecha. La gráfica no corta la asíntota vertical. Nos unen ahora a los diferentes puntos de una curva suave.

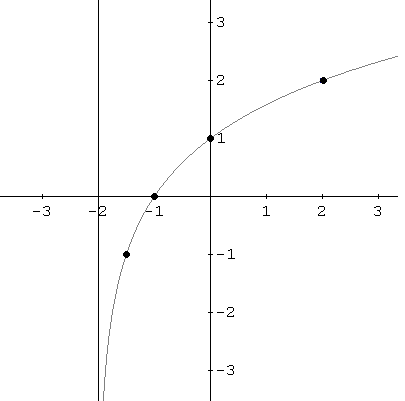
f es una función dada por

f (x) = -3ln (x - 4)

Determine el dominio de f y el rango de f.
Encuentra la asíntota vertical de la gráfica de f.
Encuentra la X y la intercepta y de la gráfica de f si los hay.
Dibuje la gráfica de f.

Respuesta a la Ejemplo 2

a - El dominio de f es el conjunto de todos los valores de x tal que

x - 4 > 0

x > 4

El rango de f es el intervalo (-inf, + inf).

b - La asíntota vertical se obtiene mediante la solución de

x - 4 = 0

x = 4

Cuando x tiende a 4 de la derecha (x> 4), f (x) crece sin límite. ¿Cómo sabemos esto?

Veamos algunos valores:

f (5) = ln (5-4) =-3ln (1) = 0

f (4,001) =-3ln (0,001), que es aproximadamente igual a 20,72.

f (4.000001) =-3ln (0,000001), que es aproximadamente igual a 41,45.

c - Para encontrar la intersección x tenemos que resolver la ecuación f (x) = 0

-3ln(x - 4) = 0

Divide ambos lados por -3 a obtener

ln (x - 4) = 0

Usar las propiedades de las funciones logarítmicas y exponenciales para escribir la ecuación anterior como

e ^{ln (x - 4)} = e ⁰

Luego de simplificar

x - 4 = 1

x = 5

La x es interceptar en (5, 0).

La intersección está dada por (0, f (0)). f (0) no está definido ya que x = 0 no es un valor en el dominio de f. No hay ninguna intersección.

d - Hasta ahora tenemos el dominio, rango, x interceptar y la asíntota vertical. Necesitamos puntos extra para poder gráfico de f.

f (4,5) =-3ln (4,5 - 4) aproximadamente igual a 2,08

F (8) =-3ln (8 - 4) aproximadamente igual a - 4,16

f (14) =-3ln (14 - 4) aproximadamente igual a - 6,91

Veamos ahora esbozar todos los puntos y la asíntota vertical. Únete a los puntos por una curva suave y F aumenta a medida que x se aproxima a 4 de la derecha.

f es una función dada por

f (x) = 2ln (| X |)

Determine el dominio de f y el rango de f.
Encuentra la asíntota vertical de la gráfica de f.
Encuentra la X y la intercepta y de la gráfica de f si los hay.
Dibuje la gráfica de f.

Respuesta a la Ejemplo 3

a - El dominio de f es el conjunto de todos los valores de x tal que

|x| > 0

El dominio es el conjunto de todos los números reales excepto 0.

El rango de f es el intervalo (-inf, + inf).

b - La asíntota vertical se obtiene mediante la solución de

|x| = 0

lo que da

x = 0

Cuando x tiende a 0 por la derecha (x> 0), f (x) decrece sin límite. ¿Cómo sabemos esto?

Veamos algunos valores:

f (1) = 2 ln (| 1 |) = 0

f (0,1) = 2ln (0,1), que es aproximadamente igual a -4,61.

f (0,0001) = 2ln (0,0001), que es aproximadamente igual a -18,42.

f (0.0000001) = 2ln (0,0000001), que es aproximadamente igual a -32,24.

Cuando x se aproxima a 0 por la izquierda (x <0), f (x) decrece sin límite. ¿Cómo sabemos esto?

Veamos algunos valores:

f (-1) = 2 ln (| -1 |) = 0

f (-0,1) = 2ln (| -0,1 |), que es aproximadamente igual a -4,61.

f (-0,0001) = 2ln (| -0,0001 |), que es aproximadamente igual a -18,42.

f (-0.0000001) = 2ln (| -0,0000001 |), que es aproximadamente igual a -32,24.

c - Para encontrar la intersección x tenemos que resolver la ecuación f (x) = 0

2ln (| X |) = 0

Divide ambos lados por 2 para obtener

ln (| X |) = 0

Usar las propiedades de las funciones logarítmicas y exponenciales para escribir la ecuación anterior como

e ^{ln (| X |)} = e ⁰

Luego de simplificar

| X | = 1

Dos x intercepta en (1, 0) y (-1, 0).

La intersección está dada por (0, f (0)). f (0) no está definido ya que x = 0 no es un valor en el dominio de f. No hay ninguna intersección.

d - Hasta ahora tenemos el dominio, rango, x interceptar y la asíntota vertical. Mediante el examen de la función f es fácil demostrar que esta es una función par y su gráfica es simétrica con respecto al eje y.

f (-x) = 2 ln (|-x |)

pero

|-x | = | x |

y por lo tanto

f (-x) = 2 ln (| x |) = f (x), esto demuestra que f es una función par.

Vamos a encontrar puntos extra.

f (4) = 2ln (| 4 |) aproximadamente igual a 2,77.

f (0,5) = 2ln (| 0.5 |) aproximadamente igual a - 1,39.

Como f es aún f (-4) = f (4) y f (-0,5) = f (0,5).

Veamos ahora esbozar todos los puntos, la asíntota vertical y Una los puntos por una curva suave.

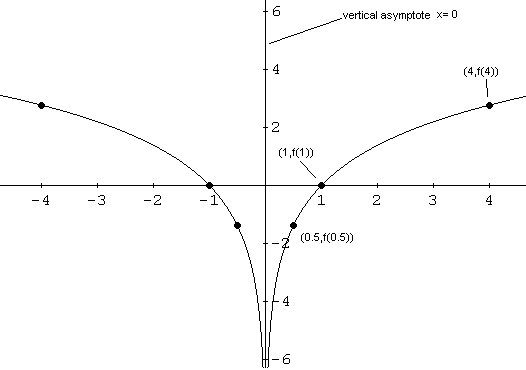
f es una función dada por

f (x) = 2 ^{(x - 2)}

Encuentra el dominio y el rango de f.
Encuentra la asíntota horizontal de la gráfica.
Encuentra la X y la intercepta y de la gráfica. de f si los hay.
Dibuje la gráfica de f.

Respuesta a la Ejemplo 1

El dominio de f es el conjunto de todos los números reales. Para encontrar el rango de f, empezamos con
Multiplica ambos lados por 2 ^-2 lo cual es positivo.

Usar las propiedades exponencial

2 ^{(x - 2)} > 0

Esta última declaración sugiere que f (x)> 0. El rango de f es (0, + inf).

Como x disminuye sin límite, f (x) = 2 ^{(x - 2)} se aproxima a 0. La gráfica de f tiene una asíntota horizontal en y = 0.

Para encontrar la intersección x tenemos que resolver la ecuación

f (x) = 0

2 ^{(x - 2)} = 0

Esta ecuación no tiene solución, consulte el rango de lo anterior, f (x)> 0. La gráfica de f no tiene una x interceptar. La intersección está dada por

(0, f (0)) = (0,2 ^{(0 - 2)}) = (0, 1 / 4).

Hasta el momento tenemos el dominio, rango, intersección y la asíntota horizontal. Necesitamos puntos extra.

(4, f (4)) = (4, 2 ^{(4 - 2)}) = (4, 2 ²) = (4, 4)

(-1, F (-2)) = (-1, 2 ^{(-1 - 2)}) = (-1, 2 ^-3) = (-1, 1 / 8)

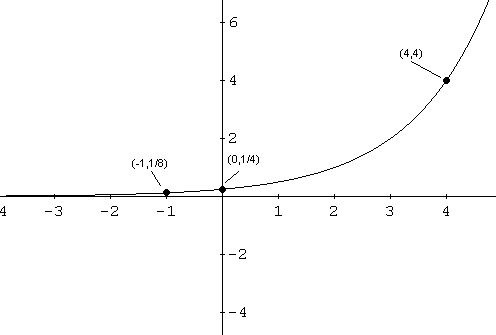
Aprovechemos ahora toda la información anterior para graficar f.

f es una función dada por

f (x) = 3 ^{(x + 1)} - 2

Encuentra el dominio y el rango de f.
Encuentra la asíntota horizontal de la gráfica de f.
Encuentra la X y la intercepta y de la gráfica de f si los hay.
Dibuje la gráfica de f.

El dominio de f es el conjunto de todos los números reales. Para encontrar el rango de f, empezamos con
Multiplica ambos lados por 3, que es positivo.
Usar las propiedades exponencial
Resta 2 a ambos lados
Esta última declaración sugiere que f (x)> -2. El rango de f es (-2, + inf).
Como x disminuye sin límite, f (x) = 3 ^{(x + 1)} -2 enfoques -2. La gráfica de f tiene una asíntota horizontal y = -2.
Para encontrar la intersección x tenemos que resolver la ecuación f (x) = 0
Añadir de 2 a ambos lados de la ecuación de
Vuelva a escribir la ecuación anterior en forma logarítmica
Resuelva para x
La intersección está dada por
Hasta el momento tenemos el dominio, rango, x e intercepta y, y la asíntota horizontal. Necesitamos puntos extra.
Aprovechemos ahora toda la información anterior para graficar f.

FUNCIÓN CONTINUA Y DESCONTINUA

Una función es continua en un punto si existe límite en él y coincide con el valor que toma la función en ese punto.
Una idea intuitiva de función continua se tiene al considerar que su gráfica es continua, en el sentido que se puede dibujar sin levantar el lápiz de la hoja de papel.
Continuidad de una función en un punto
Se dice que una función f(x) es continua en un punto x = a si y sólo si se cumplen las tres condiciones siguientes:
1. Que el punto x= a tenga imagen.
2. Que exista el límite de la función en el punto x = a.
3. Que la imagen del punto coincida con el límite de la función en el punto.

Función discontinua

Aquella que no puede dibujarse de un solo trazo. Es decir, existen puntos donde de una pequeña variación de la variable independiente produce un salto en los valores de la variable dependiente. Estos puntos reciben el nombre de puntos de discontinuidad de la función

EJERCICIOS:

Estudiar la continuidad de las siguientes funciones:

La función es continua en todos los puntos de su dominio.

D = R- {-2,2}

La función tiene dos puntos de discontinuidad en x=-2 y x=2.

ES CONTINUA

ES CONTINUA

ES DESCONTINUA

Analice la continuidad de las siguientes funciones dadas sus gráficas. En caso de que existan puntos de discontinuidad, indíquelos.

Discontinuidad de salto en x = -3. Discontinuidad evitable en x = 0.

Analice la continuidad de las siguientes funciones

a)	b)
c)	d)

a) Discontinuidad de salto en x = 0.	b) Continua en todo punto.
c) Continua en todo punto.	d) Discontinuidad de salto en x = 2.

Función inyectiva

En matemáticas, una función $f \colon X \to Y \,$ es inyectiva si a cada valor del conjunto $X\,$ (dominio) le corresponde un valor distinto en el conjunto $Y\,$ (imagen) de $f\,$ . Es decir, a cada elemento del conjunto Y le corresponde un solo valor de X tal que, en el conjunto X no puede haber dos o más elementos que tengan la misma imagen.

EJEMPLO:

Función sobreyectiva

En matemática, una función $f \colon X \to Y \,$ es sobreyectiva (epiyectiva, suprayectiva, suryectiva, exhaustiva o subyectiva), si está aplicada sobre todo el codominio, es decir, cuando cada elemento de "Y" es la imagen de como mínimo un elemento de "X".
Formalmente,

$\forall y \in Y \quad \exists x \in X : \quad f(x) = y$

Función biyectiva

En matemáticas, una función es biyectiva si es al mismo tiempo inyectiva y sobreyectiva; es decir, si todos los elementos del conjunto de salida tienen una imagen distinta en el conjunto de llegada, y a cada elemento del conjunto de llegada le corresponde un elemento del conjunto de salida.

Formalmente, dada una función $f$ :

$\begin{array}{rrcl} f : & X & \to & Y \\ & x & \to & y = f(x) \end{array}$

La función es biyectiva si se cumple la siguiente condición:

$\forall y \in Y \; : \quad \exists !\ x\in X \; / \quad f(x) = y$

Es decir, si para todo $y$ de $Y$ se cumple que existe un único $x$ de $X$ , tal que la función evaluada en $x$ es igual a $y$ .
Dados dos conjuntos $X$ e $Y$ finitos, entonces existirá una biyección entre ambos si y sólo si $X$ e $Y$ tienen el mismo número de elementos.

EJERCICIOS:

La función f(x)=x+1 es inyectiva y sobreyectiva ya que el dominio de la función es todos los reales y el rango son todos los reales, es biyectiva.

la función f(x)= $\displaystyle\frac{1}{x+1}$ es inyectiva ya que los elementos del conjunto de partida tienen distintas imágenes en el conjunto de llegada.se podría decir que es sobreyectiva también

la función f(x) = x

no es inyectiva ya que hay elementos del conjunto de partida o dominio que tienen la misma imagen. Pero solo tiene imágenes de números positivos en el rango.

Determinar si la siguiente función es o no inyectiva: f(x) = x² – 2
Asignando valores a "x" y representándolos en la tabla resulta:

x	-3	-2	-1	0	1	2	3
f(x)	5	2	-1	-2	-1	2	5

:Donde su gráfica será

Determinar si la siguiente función es o no inyectiva: g(x) = 1 – x³.Asignando valores a "x" y representándolos en la tabla resulta:

x	-3	-2	-1	0	1	2	3
f(x)	28	9	2	1	0	-7	-26

Donde su gráfica seráa:

Si la función fuera parábola, f(x)=x²como la que se muestra a continuación:

Hay elementos en el domino que se le asigna el mismo valor de la imagen; por ejemplo la pareja de valores P1(2,4) tiene el mismo valor de la imagen 4; que el punto P2(-2,4). Por lo tanto la

función

NO ES INYECTIVA.

MATEMATICAS 4°

miércoles, 27 de marzo de 2013

BLOQUE 1

f(x) = arccosen x

Función discontinua

Función inyectiva

Función sobreyectiva

Función biyectiva

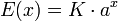
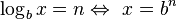
No hay comentarios.:

Publicar un comentario

Acerca de mí