FUNCIÓN INVERSA
si f es una aplicación o función que lleva elementos de I en elementos de J, en ciertas condiciones será posible definir la aplicación f -1 que realice el camino de vuelta de J a I. En ese caso diremos que f -1 es la aplicación inversa o recíproca de f.
Sea f una función real inyectiva cuyo dominio sea el conjunto I, es decir, creciente o decreciente en el conjunto I, y cuya imagen sea el conjunto J. Entonces, la función recíproca o inversa de f, denotada f -1, es la función de dominio J e imagen I definida por la siguiente regla:
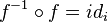 y
y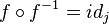 .
.
EJERCICIOS:
Si dos funciones son inversas su composición es la función identidad.
f o f -1 = f -1 o f = x
Las gráficas de f y f -1 son simétricas respecto de la bisectriz del primer y tercer cuadrante.

Hay que distinguir entre la función inversa, f−1(x), y la inversa de una función,

f o f -1 = f -1 o f = x
Las gráficas de f y f -1 son simétricas respecto de la bisectriz del primer y tercer cuadrante.

Hay que distinguir entre la función inversa, f−1(x), y la inversa de una función,

En f(x) = x2 no tiene en cuenta qué podría elegir de otra forma. Para que sea inyectiva se puede optar entre los conjuntos o , como nuevo dominio. No se puede confundir entre resolver una ecuación x2 = 9, que tiene dos soluciones , con hallar , que tiene como resultado 3.
En la función f y de su recíproca g, donde los respectivos dominios de definición son I = [^-6; 6] y j = [-6; 2]. Los gráficos que representan f y g son simétricos con relación a la primera diagonal, es decir la recta ⌂: y = x. En efecto, esta simetría envía un punto cualquiera M (x, y) sobre el punto M’ (y, x).
M pertenece a la curva de f si sólo sí M’ pertenece a la de g, porque la primera condición se escribe y = f (x) y la segunda x= g (y) y son por definición equivalentes. Las tangentes M y M’ tienen pendientes inversas. Es un efecto de la simetría anterior, y es la ilustración geométrica de la relación g’ (y) . f’ (x) = 1.
En la función f y de su recíproca g, donde los respectivos dominios de definición son I = [^-6; 6] y j = [-6; 2]. Los gráficos que representan f y g son simétricos con relación a la primera diagonal, es decir la recta ⌂: y = x. En efecto, esta simetría envía un punto cualquiera M (x, y) sobre el punto M’ (y, x).
M pertenece a la curva de f si sólo sí M’ pertenece a la de g, porque la primera condición se escribe y = f (x) y la segunda x= g (y) y son por definición equivalentes. Las tangentes M y M’ tienen pendientes inversas. Es un efecto de la simetría anterior, y es la ilustración geométrica de la relación g’ (y) . f’ (x) = 1.


Calcula la inversa de : y = 2x +7
y = 2x +7
y - 7 = 2x y -7 / 2 = x
cambiamos las variables para que se trate de la función inversa: f−1(x)= x -7 / 2
Calcula la inversa de : y = x3
y= x3
3 raiz de y = x
f−1(x)= 3 raiz de y
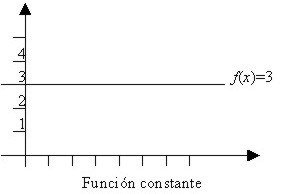
FUNCIÓN CONSTANTE.
Se llama función constante a aquella función matemática que toma el mismo valor para cualquier valor de la variable independiente. Se la representa de la forma:
la siguiente gráfica representa la recta y =
-2.


dominio-2: { xER} Contradominio { y=- 2}
de función constante es f(x) = -1:

D: { xER} CONTRA: { Y= -1 }
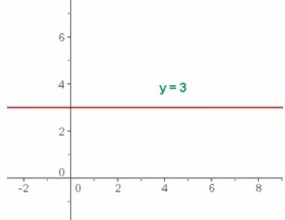
f(x) = 3,
(que corresponde al valor de y) donde el dominio es el conjunto de los números reales y el recorrido es {3}, por tanto y = 3. La gráfica de abajo muestra que es una recta horizontal.
f(x) = 3,
(que corresponde al valor de y) donde el dominio es el conjunto de los números reales y el recorrido es {3}, por tanto y = 3. La gráfica de abajo muestra que es una recta horizontal.
 |
Función identidad
En matemáticas una función identidad es una función matemática, de un conjunto M a sí mismo, que devuelve su propio argumento
La función identidad puede describirse de la forma siguiente:
Ejemplos
La función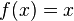 de
de  en
en  tiene como representación gráfica en el eje de coordenadas la línea recta que cruza el origen subiendo en un ángulo de 45° hacia la derecha.
tiene como representación gráfica en el eje de coordenadas la línea recta que cruza el origen subiendo en un ángulo de 45° hacia la derecha.
La función identidad en 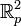 (el plano de los reales tomando las coordenadas polares) es la función determinada por la ecuación
(el plano de los reales tomando las coordenadas polares) es la función determinada por la ecuación  : una espiral que se aleja del origen uniformemente en el sentido contrario a las agujas del reloj.
: una espiral que se aleja del origen uniformemente en el sentido contrario a las agujas del reloj.
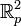 (el plano de los reales tomando las coordenadas polares) es la función determinada por la ecuación
(el plano de los reales tomando las coordenadas polares) es la función determinada por la ecuación  : una espiral que se aleja del origen uniformemente en el sentido contrario a las agujas del reloj.
: una espiral que se aleja del origen uniformemente en el sentido contrario a las agujas del reloj.
La función identidad en 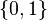 es la doble negación, expresada por
es la doble negación, expresada por 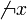 .
.
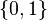 es la doble negación, expresada por
es la doble negación, expresada por 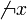 .
.
f(x) = x
Su gráfica es la bisectriz del primer y tercer cuadrante.
Por tanto la recta forma con la parte positiva del eje de abscisas un ángulo de 45º y tiene de pendiente: m = 1.

Y=3/2 x+6
el valor de b es 6. Por su parte m (pendiente) es igual a 3/2.
Cuando Y vale 0, ¿entonces X vale? Eso veremos. 0=3/2 x+6. Al despejar, pues estamos ante una ecuación de primer grado. La expresión queda de este modo. 3/2 x=-6 en este caso, multiplicamos el denominador 2, con el 6 numero libre, y obtenemos como igualdad 12, a su vez, este doce lo dividimos por en numerador que pasa a dividir, de este modo 12/3 = -4, el signo no sufre variación alguna. La respuesta definitiva es -4, lo que quiere decir que cuando Y vale 0, X vale – 4
Hemos obtenido en consecuencia. Dos pares ordenados. Estos son (0,6) & (-4,0) que son los puntos en los que la recta toca el plano cartesiano.
como sabemos que m vale 3/2, en consecuencia α valdrá 3/2. Esto se ha señalado en letras naranjas sobre el plano.
Veamos toda la operación graficada en el plano cartesiano para finiquitar el proceso de funciones lineales ejemplos.
caso particular en que a = 1, obtenemos la función identidad, es decir, f(x) = x, cuya gráfica es la bisectriz del primer y del tercer cuadrante.
Ejercicio 2f(x) = 3x - 1
caso particular en que a = 1, obtenemos la función identidad, es decir, f(x) = x, cuya gráfica es la bisectriz del primer y del tercer cuadrante.
Ejercicio 2f(x) = 3x - 1
Función escalón
La función escalón de Heaviside, también llamada función escalón unitario, debe su nombre al matemático inglés Oliver Heaviside. Es una función discontinua cuyo valor es 0 para cualquier argumento negativo, y 1 para cualquier argumento positivo:
EJERCICIOS:
La función está dada por
está dada por

y su gráfica se muestra en la figura
Cuando la función de Heaviside se multilplica por una función
se multilplica por una función  , definida
para
, definida
para  , ésta función se desactiva en el intervalo
, ésta función se desactiva en el intervalo ![$ [0,a]$](http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/EcuacionesDiferenciales/EDO-Geo/edo-cap5-geo/laplace/img334.gif) , como
muestra en siguiente ejemplo.
, como
muestra en siguiente ejemplo.
La función está dada por



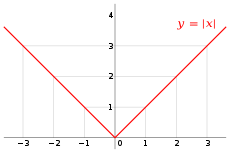
FUNCIÓN DE VALOR ABSOLUTO
La función de valor absoluto tiene por ecuación f(x) = |x|, y siempre representa distancias; por lo tanto, siempre será positiva o nula.
En esta condición, de ser siempre positiva o nula, su gráfica no se encontrará jamás debajo del eje x. Su gráfica va a estar siempre por encima de dicho eje o, a lo sumo, tocándolo.
Las funciones en valor absoluto siempre representan una distancia o intervalos (tramos o trozos) y se pueden resolver o calcular siguiendo los siguientes pasos:
1. Se iguala a cero la función, sin el valor absoluto, y se calculan sus raíces (los valores de x).
2. Se forman intervalos con las raíces (los valores de x) y se evalúa el signo de cada intervalo.
3. Definimos la función a intervalos, teniendo en cuenta que en los intervalos donde la x es negativa se cambia el signo de la función.
4. Representamos la función resultante.
Formalmente, el valor absoluto o módulo de todo número real está definido por:
está definido por:
 siempre será mayor o igual que cero y nunca negativo.
siempre será mayor o igual que cero y nunca negativo.
Desde un punto de vista geométrico, el valor absoluto de un número real es siempre positivo o cero, pero nunca negativo. En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. De hecho, el concepto de función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia, a la distancia a lo largo de la recta numérica real
es siempre positivo o cero, pero nunca negativo. En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. De hecho, el concepto de función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia, a la distancia a lo largo de la recta numérica real
EJERCICIOS:
f es una función dada por
f (x) = | x - 2 |
Solución del Ejemplo 1
EJERCICIOS:
- Trazar la gráfica de la función
 .
.
La función

y su gráfica se muestra en la figura
Cuando la función de Heaviside
- Trazar la gráfica de la función
 .
.
La función está dada por



FUNCIÓN DE VALOR ABSOLUTO
La función de valor absoluto tiene por ecuación f(x) = |x|, y siempre representa distancias; por lo tanto, siempre será positiva o nula.
En esta condición, de ser siempre positiva o nula, su gráfica no se encontrará jamás debajo del eje x. Su gráfica va a estar siempre por encima de dicho eje o, a lo sumo, tocándolo.
Las funciones en valor absoluto siempre representan una distancia o intervalos (tramos o trozos) y se pueden resolver o calcular siguiendo los siguientes pasos:
1. Se iguala a cero la función, sin el valor absoluto, y se calculan sus raíces (los valores de x).
2. Se forman intervalos con las raíces (los valores de x) y se evalúa el signo de cada intervalo.
3. Definimos la función a intervalos, teniendo en cuenta que en los intervalos donde la x es negativa se cambia el signo de la función.
4. Representamos la función resultante.
Formalmente, el valor absoluto o módulo de todo número real
 está definido por:
está definido por: siempre será mayor o igual que cero y nunca negativo.
siempre será mayor o igual que cero y nunca negativo.Desde un punto de vista geométrico, el valor absoluto de un número real
 es siempre positivo o cero, pero nunca negativo. En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. De hecho, el concepto de función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia, a la distancia a lo largo de la recta numérica real
es siempre positivo o cero, pero nunca negativo. En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. De hecho, el concepto de función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia, a la distancia a lo largo de la recta numérica realPropiedades fundamentales

No negatividad 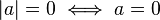
Definición positiva 
Propiedad multiplicativa 
Desigualdad triangular (Véase también Propiedad aditiva)
Otras propiedades

Simetría 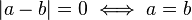
Identidad de indiscernibles 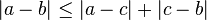
Desigualdad triangular 
(equivalente a la propiedad aditiva) 
Preservación de la división (equivalente a la propiedad multiplicativa)
EJERCICIOS:
f es una función dada por
- Encuentra la x , y intercepta de la gráfica de f.
- Encuentra el dominio y el rango de f.
- Dibuje la gráfica de f.
Solución del Ejemplo 1
- a - La intersección está dada
por (0, f (0)) = (0, | -2 |) = (0, 2)
- La coordenada x de la
intersección x es igual a la solución de la ecuación de | x - 2 | = 0que esx = 2
- La x se intercepta en el punto
(2, 0)
- b - El dominio de f es el
conjunto de todos los números reales Desde | x - 2 | puede ser positivo o cero para x = 2; el rango de f está dada por el intervalo [0, + infinito).
- c - Para dibujar la gráfica de
f (x) = | x - 2 |, nos primer esbozo de la gráfica de y = x - 2 y luego tomar el
valor absoluto de y. La gráfica de y = x - 2 es una línea de intersección con x (2, 0) y la intersección y (0, -2). (véase el gráfico más abajo)
- A continuación utilizar la definición del valor
absoluto para graficar f (x) = | x - 2 | = | y |. Si y >= 0 entonces | y | = y, si y <0 entonces | y | = -y.
- Para los valores de x para los que y es positiva,
la gráfica de | s | es la misma que la de y = x - 2. Para los valores de x para los cuales y es negativa, la gráfica de |
y | es una reflexión sobre el eje x de la gráfica de y. La gráfica de y = x - 2 arriba y se ha negativo en el intervalo
infinito (-, 2) y es esta parte de la gráfica que tiene que reflejarse en el eje
x. (véase el gráfico más abajo).

- Compruebe que el rango está dado por el intervalo [0, + infinito), el dominio es el conjunto de todos los números reales, la intersección está en (0, 2) y la intersección x en (2, 0).
- f es una función dada por
- Encuentra la x , y intercepta de la gráfica de f.
- Encuentra el dominio y el rango de f.
- Dibuje la gráfica de f.
Solución al Ejemplo 2
- a - La intersección está dada
por (0, f (0)) = (0, (-2) 2 - 4) = (0, 0)
- Las coordenadas x de las
intersecciones x son iguales a las soluciones de la ecuación de
| (x - 2) 2 - 4 | = 0que se resuelve(x - 2) 2 = 4Que da las solucionesx = 0 y x = 4
- La x se intercepta en el punto
(0, 0) y (4, 0)
- b - El dominio de f es el
conjunto de todos los números reales Desde | (x - 2)2 - 4 | puede ser positivo o cero para x = 4 y x = 0; el rango de f está dada por el intervalo [0, + infinito).
- c - Para dibujar la gráfica de
f (x) = | (x - 2)2 - 4 |, nos primer esbozo de la gráfica de y = (x -
2)2 - 4 y luego tomar el valor absoluto de y. La gráfica de y = (x - 2)2 - 4 es una parábola con vértice en (2, -4), x intercepta (0, 0) y (4, 0) y la intersección ay (0, 0). (véase el gráfico más abajo)

- La gráfica de f está dada por la reflexión sobre
parte del eje x de la gráfica de y = (x - 2) 2 - 4 para los que y es
negativa. (véase el gráfico más abajo).




D= 






D=








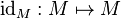







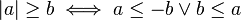
No hay comentarios.:
Publicar un comentario